
分析 根据无理数的定义,无理数常见的三种类型(1)开不尽的方根,如$\sqrt{2}$等.(2)特定结构的无限不循环小数,如0.303 003 000 300 003…(两个3之间依次多一个0).(3)含有π的绝大部分数,如2π,可得答案.
解答 解:∵$-\sqrt{2}$是无理数;$\frac{22}{7}$是有理数;$\sqrt{1.21}$=1.1,是有理数;π是无理数;$\sqrt{9}$=3,是有理数;2.121121112…是无理数;
∴在-$\sqrt{2}$,$\frac{22}{7}$,$\sqrt{1.21}$,π,$\sqrt{9}$,2.121121112…(两个2 之间的1逐次加1个)中,无理数有:$-\sqrt{2}$,π,2.121121112…,
故答案为:$-\sqrt{2}$,π,2.121121112….
点评 本题主要考查了无理数的定义,化简之后再判断是解答此题的关键.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:选择题
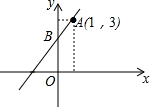 如图,直线y=kx+b经过A(1,3)和B(0,2),则关于x的不等式kx+b<3的解集是( )
如图,直线y=kx+b经过A(1,3)和B(0,2),则关于x的不等式kx+b<3的解集是( )| A. | x<1 | B. | x>1 | C. | x<0 | D. | x>0 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | ($\frac{3}{2}$,0) | B. | (-$\frac{3}{2}$,0) | C. | (0,$\frac{3}{2}$) | D. | ($\frac{2}{3}$,0) |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,在Rt△ABC中,∠C=90°,以点C为圆心作⊙C,与AB切于点D,过点A、B分别作⊙C的切线AF、BE,切点为F、E点.求证:AF∥BE.
如图,在Rt△ABC中,∠C=90°,以点C为圆心作⊙C,与AB切于点D,过点A、B分别作⊙C的切线AF、BE,切点为F、E点.求证:AF∥BE.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com