
【题目】如图,点P是正方形ABCD内一点,点P到点A、B和D的距离分别为1,2 ![]() ,
, ![]() ,△ADP沿点A旋转至△ABP′,连结PP′,并延长AP与BC相交于点Q.
,△ADP沿点A旋转至△ABP′,连结PP′,并延长AP与BC相交于点Q. 
(1)求证:△APP′是等腰直角三角形;
(2)求∠BPQ的大小.
【答案】
(1)证明:∵四边形ABCD为正方形,
∴AB=AD,∠BAD=90°,
∵△ADP沿点A旋转至△ABP′,
∴AP=AP′,∠PAP′=∠DAB=90°,
∴△APP′是等腰直角三角形
(2)解:∵△APP′是等腰直角三角形,
∴PP′= ![]() PA=
PA= ![]() ,∠APP′=45°,
,∠APP′=45°,
∵△ADP沿点A旋转至△ABP′,
∴PD=P′B= ![]() ,
,
在△PP′B中,PP′= ![]() ,PB=2
,PB=2 ![]() ,P′B=
,P′B= ![]() ,
,
∵( ![]() )2+(2
)2+(2 ![]() )2=(
)2=( ![]() )2,
)2,
∴PP′2+PB2=P′B2,
∴△PP′B为直角三角形,∠P′PB=90°,
∴∠BPQ=180°﹣∠APP′﹣∠P′PB=180°﹣45°﹣90°=45°
【解析】(1)根据正方形的性质得AB=AD,∠BAD=90°,再利用旋转的性质得AP=AP′,∠PAP′=∠DAB=90°,于是可判断△APP′是等腰直角三角形;(2)根据等腰直角三角形的性质得PP′= ![]() PA=
PA= ![]() ,∠APP′=45°,再利用旋转的性质得PD=P′B=
,∠APP′=45°,再利用旋转的性质得PD=P′B= ![]() ,接着根据勾股定理的逆定理可证明△PP′B为直角三角形,∠P′PB=90°,然后利用平角定义计算∠BPQ的度数.
,接着根据勾股定理的逆定理可证明△PP′B为直角三角形,∠P′PB=90°,然后利用平角定义计算∠BPQ的度数.
【考点精析】通过灵活运用等腰直角三角形和正方形的性质,掌握等腰直角三角形是两条直角边相等的直角三角形;等腰直角三角形的两个底角相等且等于45°;正方形四个角都是直角,四条边都相等;正方形的两条对角线相等,并且互相垂直平分,每条对角线平分一组对角;正方形的一条对角线把正方形分成两个全等的等腰直角三角形;正方形的对角线与边的夹角是45o;正方形的两条对角线把这个正方形分成四个全等的等腰直角三角形即可以解答此题.


 智趣寒假作业云南科技出版社系列答案
智趣寒假作业云南科技出版社系列答案科目:初中数学 来源: 题型:
【题目】一个口袋中有9个红球和若干个白球,在不允许将球倒出来数的前提下,小明采用如下的方法估算其中白球的个数:从口袋中随机摸出一球,记下颜色,然后把它放回口袋中,摇匀后再随机摸出一球,记下颜色…,小明重复上述过程共摸了100次,其中40次摸到白球,请回答:
(1)口袋中的白球约有多少个?
(2)有一个游乐场,要按照上述红球、白球的比例配置彩球池,若彩球池里共有1200个球,则需准备多少个红球?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AB=BC,BE⊥AC于点E,AD⊥BC于点D,
∠BAD=45°,AD与BE交于点F,连接CF.

(1)求证:BF=2AE;
(2)若CD=![]() ,求AD的长.
,求AD的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在数学活动课中,小辉将边长为![]() 和3的两个正方形放置在直线l上,如图1,他连结AD、CF,经测量发现AD=CF.
和3的两个正方形放置在直线l上,如图1,他连结AD、CF,经测量发现AD=CF.
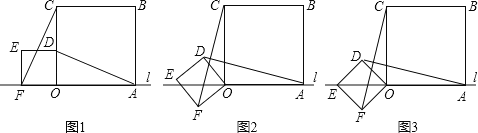
(1)他将正方形ODEF绕O点逆时针旋转一定的角度,如图2,试判断AD与CF还相等吗?说明你的理由;
(2)他将正方形ODEF绕O点逆时针旋转,使点E旋转至直线l上,如图3,请你求出CF的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,四边形ABCD中,AC,BD相交于点O,O是AC的中点,AD//BC,AC=8,BD=6.
(1)求证:四边形ABCD是平行四边形;
(2)若AC⊥BD,求□ABCD的面积.

查看答案和解析>>
科目:初中数学 来源: 题型:
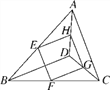
【题目】如图,E,F,G,H分别是边AB,BC,CD,DA的中点,连接EF,FG,GH,HE.
(1)判断四边形EFGH的形状,并证明你的结论;
(2)当BD,AC满足什么条件时,四边形EFGH是正方形?请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】探索题
图a是一个长为2m、宽为2n的长方形,沿图中虚线用剪刀均分成四块小长方形,然后按图b的形状拼成一个正方形.

(1)你认为图b中的影部分的正方形的边长等于 .
(2)请用两种不同的方法求图b中阴影部分的面积.
方法1: (只列式,不化简)
方法2: (只列式,不化简)
(3)观察图b你能写出下列三个代数式之间的等量关系吗?
代数式:(m+n)2,(m-n)2,![]() .
.
(4)根据(3)题中的等量关系,解决如下问题:若a+b=8,ab=5,则 (a-b)2= .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一个不透明的口袋里装有分别标有汉字“美”、“丽”、“南”、“山”的四个小球,除汉字不同之外,小球没有任何区别,每次摸球前先搅拌均匀再摸球.
(1)若从中任取一个球,求摸出球上的汉字刚好是“美”的概率;
(2)甲从中任取一球,不放回,再从中任取一球,请用树状图或列表法,求甲取出的两个球上的汉字恰能组成“美丽”或“南山”的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
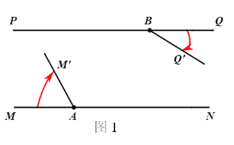
【题目】如图1,直线MN//直线PQ,点A、B分别是直线MN、PQ上的两点.将射线AM绕点A顺时针匀速旋转,射线BQ绕点B顺时针匀速旋转,旋转后的射线分别记为AM′、BQ′,已知射线AM、射线BQ旋转的速度之和为7度/秒.
(1)如果射线BQ 先转动30°后,射线AM、BQ′再同时旋转10秒时,射线AM′与BQ′第一次出现平行.求射线AM、BQ的旋转速度;
(2)若射线AM、BQ分别以(1)中速度同时转动t秒,在射线AM′与AN重合之前,求t为何值时AM′⊥BQ′;
(3)若∠BAN=45°,射线AM、BQ分别以(1)中的速度同时转动t秒,在射线AM′与AN重合之前,射线AM′与BQ′交于点H,过点H作HC⊥PQ,垂足为C,如图2所示,设∠BAH=α,∠BHC=β,求α和β满足的数量关系,直接写出结果.


查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com