
�ۺ���ʵ��
�����Ķ� ������ǧ����ǰ���ҹ��ܳ���ѧ���̸߾��������һ��ֱ���۳�һ��ֱ�ǣ���������������ɵ����ģ���ô�Ҿ͵����壬�������������ģ����塱�������������ҹ��Ŵ�������ѧ�����������㾭���У�Ϊ�˷��㣬�ڱ����У����ǰ����ߵı�Ϊ3��4��5�������γ�Ϊ��3��4��5���������Σ����磺���߳��ֱ�Ϊ9��12��15�� �������ξ��ǣ�3��4��5���������Σ��þ���ֽƬ������IJ������������۳��������͵������Σ�
�������ξ��ǣ�3��4��5���������Σ��þ���ֽƬ������IJ������������۳��������͵������Σ�
ʵ������ ��ͼ1���ھ���ֽƬABCD�У�AD=8cm��AB=12cm��
��һ������ͼ2����ͼ1�еľ���ֽƬABCD�ع���A��ֱ���۵���ʹ��D����AB�ϵĵ�E�����ۺ�ΪAF������EF�۵���Ȼ���ֽƬչƽ��
�ڶ�������ͼ3����ͼ2�еľ���ֽƬ�ٴ��۵���ʹ��D���F�غϣ��ۺ�ΪGH��Ȼ��չƽ����ȥAF��
����������ͼ4����ͼ3�еľ���ֽƬ��AH�۵����õ���AD��H������AD���۵����ۺ�ΪAM��AM���ۺ�EF���ڵ�N��Ȼ��չƽ��

������
��1������ͼ2��֤���ı���AEFD�������Σ�
��2������ͼ4���ж�NF��ND���������ϵ��������֤����
��3������ͼ4��֤����AEN�ǣ�3��4��5���������Σ�
̽������
��4���ڲ�������ĸ������£�ͼ4�л�����Щ�������ǣ�3��4��5���������Σ����ҳ���ֱ��д�����ǵ����ƣ�

| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ��2017����б�ҵ��ѧ���ԣ�ɽ�����ݾ�����ѧ�������棩 ���ͣ������
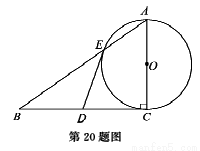
��ͼ����֪Rt��ABC,��C=90�㣬DΪBC���е�.��ACΪֱ����ԲO��AB�ڵ�E.
��1����֤��DE��ԲO������.
(2)��AE:EB=1:2,BC=6����AE�ij�.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ��2017����б�ҵ��ѧ���ԣ��Ϻ�������ѧ�������棩 ���ͣ�ѡ����
���һ�κ���y=kx+b��k��b�dz�����k��0����ͼ����һ�����������ޣ���ôk��bӦ����������ǣ� ��
A��k��0����b��0 B��k��0����b��0 C��k��0����b��0 D��k��0����b��0
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ��2017����б�ҵ��ѧ���ԣ�����������ѧ�������棩 ���ͣ������
��ʵ����5���� ��0���У�
��0���У� �У�����һ������ ��
�У�����һ������ ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ��2017����б�ҵ��ѧ���ԣ�����������ѧ�������棩 ���ͣ�ѡ����
��ͼ��ֱ��a��b��Rt��ABC��ֱ�Ƕ���B����ֱ��a�ϣ�����1=25�㣬���2�Ĵ�СΪ�� ��
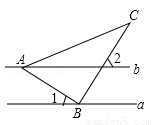
A��55�� B��75�� C��65�� D��85��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ��2017����б�ҵ��ѧ���ԣ�ɽ��������ѧ�������棩 ���ͣ������
��֪����ͼ����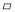 ABCD�У��ӳ���AB����E���ӳ�CD����F��ʹ��BE=DF������EF����Խ���AC���ڵ�O����֤��OE=OF��
ABCD�У��ӳ���AB����E���ӳ�CD����F��ʹ��BE=DF������EF����Խ���AC���ڵ�O����֤��OE=OF��

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ��2017����б�ҵ��ѧ���ԣ�ɽ��������ѧ�������棩 ���ͣ�ѡ����
��ͼ��ij��Ʒ�ı�־ͼ����AC��BD�ǡ�O������ֱ������β˳�����ӵ�A��B��C��D���õ��ı���ABCD����AC=10cm����BAC=36�㣬��ͼ����Ӱ���ֵ����Ϊ�� ��

A�� B��
B�� C��
C�� D��
D��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ��2017����б�ҵ��ѧ���ԣ�ɽ���Ͳ�������ѧ�������棩 ���ͣ������
�ڱ߳�Ϊ4�ĵȱ�������ABC�У�DΪBC���ϵ�����һ�㣬����D�ֱ���DE��AB��DF��AC������ֱ�ΪE��F����DE+DF= ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ��2017����б�ҵ��ѧ���ԣ��Ĵ����ݾ�����ѧ�������棩 ���ͣ������
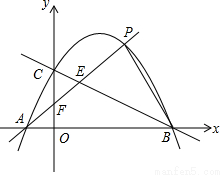
��ͼ����֪���κ���y=ax2+bx+c��a��0����ͼ��A��-1��0����B��4��0����C��0��2�����㣮
��1����ö��κ����Ľ���ʽ��
��2����D�Ǹö��κ���ͼ���ϵ�һ�㣬�������DBA=��CAO��O������ԭ�㣩�����D�����ꣻ
��3����P�Ǹö��κ���ͼ����λ��һ�����ϵ�һ���㣬����PA�ֱ�BC��y�����E��F������PEB����CEF������ֱ�ΪS1��S2����S1-S2�����ֵ��
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com