
【题目】如图,AB是⊙O的直径,点C是BA延长线上一点,CD切⊙O于点D,弦DE∥CB,Q是AB上的一点,CA=1,CD=![]() OA.
OA.
(1)求⊙O的半径R;
(2)求图中阴影部分的面积.

【答案】(1)1;(2)![]()
【解析】分析:(1)连接OD.根据切线的性质推知△CDO是直角三角形,然后在直角△CDO中利用勾股定理来求⊙O的半径R;
(2)据弦DE∥CB,可以连接OE,则阴影部分的面积就转化为扇形ODE的面积.所以阴影部分的面积不变.只需根据直角三角形的边求得角的度数即可.
详解:(1)连接OD.

∵CD切⊙O于点D,
∴OD⊥CD,即∠CDO=90°,
∴CD2+OD2=(CA+OA)2,
∵CA=1,CD=![]() OA,OD=OA,
OA,OD=OA,
∴OA=1,即R=1;
(2)连接OE.
∵DE∥CB,
∴S△ODE=S△QDE;
∴S阴影=S扇形ODE;
由(1)知,∠CDO=90°,R=1,
∴DO:CO=1:2,
∴∠DCO=30°,
∴∠COD=60°,
∴∠ODE=60°,
∴△ODE是等边三角形;
∴S阴影=S扇形ODE=![]() .
.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】在![]() 中,
中,![]() ,
,![]() ,直线l经过顶点C,过A,B两点分别作l的垂线AE,BF,垂足分别为E.F.
,直线l经过顶点C,过A,B两点分别作l的垂线AE,BF,垂足分别为E.F.
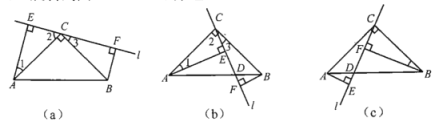
(1)如图所示,当直线l不与底边AB相交时,求证:![]() .
.
(2)当直线l绕点C旋转到图(b)的位置时,猜想EF、AE、BF之间的关系,并证明.
(3)当直线l绕点C旋转到图(c)的位置时,猜想EF、AE、BF之间的关系,直接写出结论.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,数轴上的![]() 三点所表示的数是分别
三点所表示的数是分别![]() ,其中
,其中![]() ,如果
,如果![]() ,那么该数轴的原点
,那么该数轴的原点![]() 的位置应该在( )
的位置应该在( )
![]()
A.点![]() 的左边B.点
的左边B.点![]() 与点
与点![]() 之间
之间
C.点![]() 与点
与点![]() 之间D.点
之间D.点![]() 与点
与点![]() 之间(靠近
之间(靠近![]() 点)或点
点)或点![]() 的右边
的右边
查看答案和解析>>
科目:初中数学 来源: 题型:
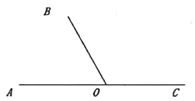
【题目】如图,在平面内,点![]() 是直线
是直线![]() 上一点,
上一点,![]() ,射线
,射线![]() 不动,射线
不动,射线![]() ,
,![]() 同时开始绕点
同时开始绕点![]() 顺时针转动,射线
顺时针转动,射线![]() 首次回到起始位置时两线同时停止转动,射线
首次回到起始位置时两线同时停止转动,射线![]() ,
,![]() 的转动速度分别为每秒
的转动速度分别为每秒![]() 和每秒
和每秒![]() .若转动
.若转动![]() 秒时,射线
秒时,射线![]() ,
,![]() ,
,![]() 中的一条是另外两条组成角的角平分线,则
中的一条是另外两条组成角的角平分线,则![]() ______秒.
______秒.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,⊙O的半径OD⊥弦AB于点C,连结AO并延长交⊙O于点E,连结EC.若AB=8,CD=2,则EC的长为( )

A. 2![]() B. 8 C. 2
B. 8 C. 2![]() D. 2
D. 2![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某超市为加快资金回笼,特推出如下优惠方案:
①一次购买价值不超过200元的商品,不享受优惠;
②一次购买价值超过200元,但不超过500元的商品,一律九折;
③一次购买价值超过500元的商品,一律八折.
根据以上方案解决下列问题:
(1)若某人一次购买价值350元的商品,则实际应付款 元(直接填空);
(2)某人一次购买了价值![]() 元的商品,实际付款432元,求
元的商品,实际付款432元,求![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某种水果第一天以2元/斤的价格卖出a斤,第二天以1.5元/斤的价格卖出b斤第三天以1.2元/斤的价格卖出c斤,求:
(1)这三天一共卖出水果多少斤?
(2)这三天一共卖得多少钱?
(3)这三天平均售价是多少?并计算当a=30,b=40,c=45时,平均售价是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,某港口P位于东西方向的海岸线上,“远航”号、“海天”号轮船同时离开港口,各自沿一固定方向航行,“远航”号每小时航行16海里,“海天”号每小时航行12海里.它们离开港口一个半小时后,分别位于点Q、R处,且相距30海里,如果知道“远航”号沿北偏东![]() 方向航行,请求出“海天”号的航行方向?
方向航行,请求出“海天”号的航行方向?

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com