
【题目】如图,已知抛物线与x交于A(﹣1,0)、E(3,0)两点,与y轴交于点B(0,3).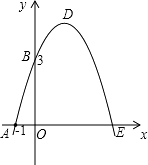
(1)求抛物线的解析式;
(2)设抛物线顶点为D,求四边形AEDB的面积.
【答案】
(1)
解:设抛物线的解析式为:y=a(x+1)(x﹣3),则有:
a(0+1)(0﹣3)=3,a=﹣1;
∴抛物线的解析式为:y=﹣x2+2x+3
(2)
解:由(1)知:y=﹣x2+2x+3=﹣(x﹣1)2+4,
即D(1,4);
过D作DF⊥x轴于F;
S四边形AEDB=S△AOB+S△DEF+S梯形BOFD= ![]() ×1×3+
×1×3+ ![]() ×2×4+
×2×4+ ![]() ×(3+4)×1=9;
×(3+4)×1=9;
即四边形AEDB的面积为9.
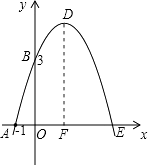
【解析】(1)已知了抛物线图象上的三点坐标,可用待定系数法求出抛物线的解析式;(2)根据抛物线的解析式,易求得抛物线顶点D的坐标;过D作DF⊥x轴于F,那么四边形AEDB的面积就可以由△AOB、△DEF、梯形BOFD的面积和求得.
【考点精析】认真审题,首先需要了解二次函数的图象(二次函数图像关键点:1、开口方向2、对称轴 3、顶点 4、与x轴交点 5、与y轴交点),还要掌握二次函数的性质(增减性:当a>0时,对称轴左边,y随x增大而减小;对称轴右边,y随x增大而增大;当a<0时,对称轴左边,y随x增大而增大;对称轴右边,y随x增大而减小)的相关知识才是答题的关键.


科目:初中数学 来源: 题型:
【题目】在学校开展的小制作评比活动中,二年级六个班都参加了比赛,根据他们上交作品的件数,绘制直方图如右.已知从左至右各长方形高的比为2∶3∶4∶2∶3∶1,小制作件数最多的三班上交了16件.经评选各班获奖件数如下表:

在这次评选中,获奖率最高的两个班级依次是( ).
A. 5班、3班 B. 3班、4班 C. 5班、6班 D. 6班、5班
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知AOB是一条直线,∠1=∠2,∠3=∠4,∠AOF=∠BOF=90°.则
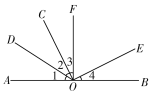
(1)∠AOC的补角是_____;
(2)____是∠AOC的余角;
(3)∠COF的补角是___.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在Rt△ABC中,∠C=90°,∠A、∠B、∠C的对边分别为a、b、c.
(1)若a∶b=3∶4,c=75cm,求a、b;
(2)若a∶c=15∶17,b=24,求△ABC的面积;
(3)若c-a=4,b=16,求a、c;
(4)若∠A=30°,c=24,求c边上的高hc;
(5)若a、b、c为连续整数,求a+b+c.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某文具店购进一批纪念册,每本进价为20元,出于营销考虑,要求每本纪念册的售价不低于20元且不高于28元,在销售过程中发现该纪念册每周的销售量y(本)与每本纪念册的售价x(元)之间满足一次函数关系:当销售单价为22元时,销售量为36本;当销售单价为24元时,销售量为32本.
(1)请直接写出y与x的函数关系式;
(2)当文具店每周销售这种纪念册获得150元的利润时,每本纪念册的销售单价是多少元?
(3)设该文具店每周销售这种纪念册所获得的利润为w元,将该纪念册销售单价定为多少元时,才能使文具店销售该纪念册所获利润最大?最大利润是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图:扇形DOE的圆心角为直角,它的半径为2cm,正方形OABC内接于扇形,点A、B、C分别在OE、 ![]() 、OD上,过E作EF⊥OE交CB的延长线于F,则图中阴影部分的面积为cm2 .
、OD上,过E作EF⊥OE交CB的延长线于F,则图中阴影部分的面积为cm2 . 
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com