练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情
    12．先化简，再求值．若|3b-2|+|2a-b|=0，求5（2a-b）-2（6a-2b+2）+（4a-3b+$\frac{1}{2}$）的值．

    分析 根据绝对值的非负性求出a、b的值，根据去括号法则和合并同类项法则把原式化简，代入计算即可．

    解答 解：由题意得，3b-2=0，2a-b=0，
    解得，b=$\frac{2}{3}$，a=$\frac{1}{3}$，
    原式=10a-5b-12a+4b-4+4a-3b+$\frac{1}{2}$
    =2a-4b-$\frac{7}{2}$
    =2×$\frac{1}{3}$-4×$\frac{2}{3}$-$\frac{7}{2}$
    =-$\frac{11}{2}$．

    点评 本题考查的是整式的加减和非负数的性质，掌握去括号法则和合并同类项法则是解题的关键，注意绝对值的非负性的应用．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：选择题

    18．学校广播站要招聘1名记者，小亮和小丽报名参加了3项素质测试，成绩如下：
    写作能力普通话水平计算机水平
    小亮90分75分51分
    小丽60分84分72分
    将写作能力、普通话水平、计算机水平这三项的总分由原先按3：5：2计算，变成按5：3：2计算，总分变化情况是（　　）
    A．小丽增加多B．小亮增加多
    C．两人成绩不变化D．变化情况无法确定

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    19．如图，在平面直角坐标系中，以A（5，1）为圆心，以2个单位长度为半径的⊙A交x轴于点B、C．解答下列问题：
    （1）根据A点坐标建立平面直角坐标系；
    （2）将⊙A向左平移3个单位长度与y轴首次相切，得到⊙A′，并画出⊙A′．此时点A′的坐标为（2，1）．
    （3）求BC的长．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

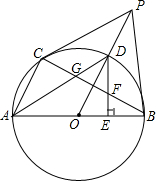    16．如图，AB为直径，PB为切线，点C在⊙O上，AC∥OP，连接OP，交⊙O点D，交BC于点H，过D点作DE⊥AB，E为垂足，交BC于点F，连AD交BC于G
    （1）求证：PC为⊙O的切线；
    （2）证明：CG=2EF；
    （3）若CG=3，DE=4，连接BD，求$\frac{DG}{DB}$的值．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    7．如图，填在下面各正方形中的四个数之间都有相同的规律，根据这种规律，求出m的值．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    17．请观察你家里的日历，并注意发现其中的规律，用你观察到的规律解答问题．
    一张空白日历，如图：

    一个直角三角形框住了6个数，只知道两直角边上6个数之和与斜边上3个数之和的差是78．
    （1）请你通过计算，将这张日历重现；
    （2）该月可能有多少天？

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    4．先化简，再求值：
    （1）-3a2（a-2b）-3b（2a2-b），其中a=$\frac{1}{3}$，b=-$\frac{1}{3}$；
    （2）m2（m+3）+2m（m2-1）-3m（m2+m-1），其中m=$\frac{2}{5}$．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    1．已知：在Rt△ABC中，∠ABC=90°，∠C=60°，现将一个足够大的直角三角形的顶点P放在斜边AC上．
    （1）设三角板的两直角边分别交边AB，BC于点M，N．
    ①当点P是AC的中点时，分别作PE⊥AB于点E，PF⊥BC于点F，得到图1，写出图中的一对全等三角形；
    ②在①的条件下，写出与△PEM相似的三角形，并直接写出PN与PM的数量关系．
    （2）移动点P，使AP=2CP，将三角板绕点P旋转，设旋转过程中三角板的两直角边分别交边AB，BC于点M，N（PM不与边AB垂直，PN不与边BC垂直）；或者三角板的两直角边分别交边AB，BC的延长线于点M，N．
    ①请在备用图中画出图形，判断PM与PN的数量关系，并选择其中一种图形证明你的结论；
    ②在①的条件下，当△PCN是等腰三角形时，若BC=3cm，则线段BN的长是1cm或5cm．

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

    2．用配方法解方程x2+8x-7=0，则配方正确的是（　　）
    A．（x+4）2=23B．（x-4）2=23C．（x-8）2=49D．（x+8）2=64

    查看答案和解析>>

    同步练习册答案