
【题目】已知:如图,在△ABC中,∠B=90![]() ,∠ACB=30
,∠ACB=30![]() ,AB=2,AD=2AC,DC=2BC.
,AB=2,AD=2AC,DC=2BC.
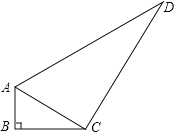
(1)求证:△ACD为直角三角形;(2)求四边形ABCD的面积.
【答案】(1)证明见解析;(2)![]() .
.
【解析】
(1)根据勾股定理求出BC的长度,再根据勾股定理逆定理得出△ACD为直角三角形;
(2)根据四边形ABCD的面积=△ABC的面积+△ACD的面积,列式进行计算即可得解.
(1)在Rt△ABC中,∵∠ACB=30°,AB=2,∴AC=2AB=4(在直角三角形中,如果一个锐角等于30°,那么它所对的直角边等于斜边的一半).
在Rt△ABC中,∵∠B=90°,∴BC2+AB2=AC2(勾股定理),∴![]() .
.
∵AD=2AC,DC=2BC,∴AD=8,![]() ,∴AC2+CD2=16+48=64,AD2=64,∴AD2=AC2+CD2,∴△ACD为直角三角形,∠ACD=90°(勾股定理逆定理).
,∴AC2+CD2=16+48=64,AD2=64,∴AD2=AC2+CD2,∴△ACD为直角三角形,∠ACD=90°(勾股定理逆定理).
(2)∵S四边形ABCD=S△ABC+S△ACD,∴![]() .
.


科目:初中数学 来源: 题型:
【题目】如图,小聪将三角尺Rt△ABC绕点C逆时针方向旋转到△DEC的位置,其中∠A为30°,∠B为直角,若点A、C、E在一条直线上,则此次旋转变换中旋转角的度数为____.
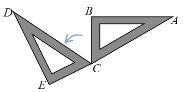
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图(1),在矩形![]() 中,
中,![]() 分别是
分别是![]() 的中点,作射线
的中点,作射线![]() ,连接
,连接![]() .
.
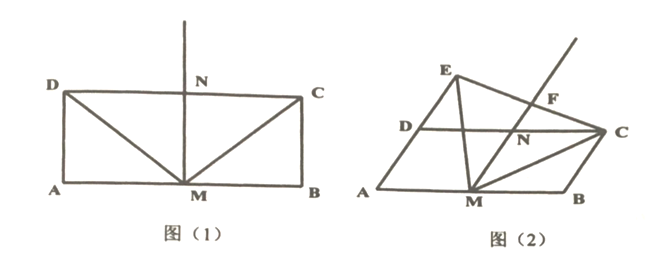
(1)请直接写出线段![]() 与
与![]() 的数量关系;
的数量关系;
(2)将矩形![]() 变为平行四边形,其中
变为平行四边形,其中![]() 为锐角,如图(2),
为锐角,如图(2),![]() ,
,![]() 分别是
分别是![]() 的中点,过点
的中点,过点![]() 作
作![]() 交射线
交射线![]() 于点
于点![]() ,交射线
,交射线![]() 于点
于点![]() ,连接
,连接![]() ,求证:
,求证:![]() ;
;
(3)写出![]() 与
与![]() 的数量关系,并证明你的结论.
的数量关系,并证明你的结论.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在纸面上有一数轴如图所示.

尝试:折叠纸面,使表示1的点与表示![]() 的点重合,则表示
的点重合,则表示![]() 的点与表示_________的点重合.
的点与表示_________的点重合.
发现:折叠纸面,使表示![]() 的点与表示3的点重合,则表示5的点与表示____________的点重合.
的点与表示3的点重合,则表示5的点与表示____________的点重合.
应用:若数轴上![]() 、
、![]() 两点之间的距离为11(
两点之间的距离为11(![]() 在
在![]() 左侧),且经过折叠后,表示
左侧),且经过折叠后,表示![]() 的点与表示3的点重合,点
的点与表示3的点重合,点![]() 与点
与点![]() 重合,分别求
重合,分别求![]() 、
、![]() 两点表示的数.
两点表示的数.
查看答案和解析>>
科目:初中数学 来源: 题型:
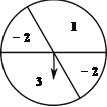
【题目】如图,可以自由转动的转盘被它的两条直径分成了四个分别标有数字的扇形区域,其中标有数字“1”的扇形圆心角为120°.转动转盘,待转盘自动停止后,指针指向一个扇形的内部,则该扇形内的数字即为转出的数字,此时,称为转动转盘一次(若指针指向两个扇形的交线,则不计转动的次数,重新转动转盘,直到指针指向一个扇形的内部为止)
(1)转动转盘一次,求转出的数字是-2的概率;
(2)转动转盘两次,用树状图或列表法求这两次分别转出的数字之积为正数的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
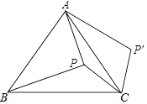
【题目】如图,点P在等边△ABC的内部,且PC=6,PA=8,PB=10,将线段PC绕点C顺时针旋转60°得到P'C,连接AP',则sin∠PAP'的值为________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某次篮球联赛初赛阶段,每队有![]() 场比赛,每场比赛都要分出胜负,每队胜一场得
场比赛,每场比赛都要分出胜负,每队胜一场得![]() 分, 负一场得
分, 负一场得![]() 分,积分超过
分,积分超过![]() 分才能获得参赛资格.
分才能获得参赛资格.
(1)已知甲队在初赛阶段的积分为![]() 分,求甲队初赛阶段胜、负各多少场;
分,求甲队初赛阶段胜、负各多少场;
(2)如果乙队要获得参加决赛资格,那么乙队在初赛阶段至少要胜多少场?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】南江县某乡![]() 两村盛产凤柑,
两村盛产凤柑,![]() 村有凤柑200吨,
村有凤柑200吨,![]() 村有凤柑300吨.现将这些凤柑运到
村有凤柑300吨.现将这些凤柑运到![]() 两个冷藏仓库,已知
两个冷藏仓库,已知![]() 仓库可储存240吨,
仓库可储存240吨,![]() 仓库可储存260吨;从
仓库可储存260吨;从![]() 村运往
村运往![]() 两处的费用分别为每吨20元和25元,从
两处的费用分别为每吨20元和25元,从![]() 村运往
村运往![]() 两处的费用分别为每吨15元和18元.设从
两处的费用分别为每吨15元和18元.设从![]() 村运往
村运往![]() 仓库的凤柑重量为
仓库的凤柑重量为![]() 吨.
吨.
(1)请填写表格(单位:吨)
(2)请分别求出![]() 两村运往两仓库的凤柑的运输费用(用含
两村运往两仓库的凤柑的运输费用(用含![]() 的代数式表示);
的代数式表示);
(3)当![]() 时,试求
时,试求![]() 两村运往两仓库的凤柑的运输费用.
两村运往两仓库的凤柑的运输费用.
|
| 总计 | |
|
| 200 | |
| 300 | ||
总计 | 240 | 260 | 500 |
查看答案和解析>>
科目:初中数学 来源: 题型:
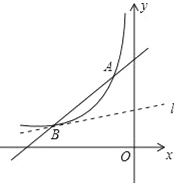
【题目】(2016广东省茂名市)如图,一次函数y=x+b的图象与反比例函数![]() (k为常数,k≠0)的图象交于点A(﹣1,4)和点B(a,1).
(k为常数,k≠0)的图象交于点A(﹣1,4)和点B(a,1).
(1)求反比例函数的表达式和a、b的值;
(2)若A、O两点关于直线l对称,请连接AO,并求出直线l与线段AO的交点坐标.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com