
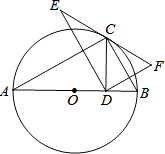
 如图,点C在以AB为直径的⊙O上,∠CAB=30°,点D在AB上由点B开始向点A运动,点E与点D关于AC对称,DF⊥DE于点D,并交EC的延长线于点F.
如图,点C在以AB为直径的⊙O上,∠CAB=30°,点D在AB上由点B开始向点A运动,点E与点D关于AC对称,DF⊥DE于点D,并交EC的延长线于点F.分析 (1)根据轴对称的性质得到∠ECA=∠DCA,根据直角三角形两锐角互余得到∠CDF=∠F,得到CD=CF,证明结论;
(2)连接OC,根据等边三角形的性质和直角三角形的性质证明∠ECO=90°,根据切线的判定定理证明即可.
解答 (1)证明:∵点E与点D关于AC对称,
∴CE=CD,
∴∠ECA=∠DCA,
又∵DF⊥DE,
∴∠CDF=90°-∠CDE=90°-∠E=∠F,
∴CD=CF,
∴CE=CF;
(2)证明:连接OC,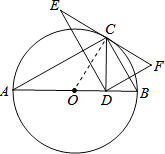
∵∠ACB=90°,∠CAB=30°,
∴∠CBA=60°,
∵OB=OC,
∴△BOC是等边三角形,
∴∠OCB=60°,
∵CD⊥AB,
∴∠OCD=∠DCB=30°,
∵点E与点D关于AC对称,
∴CD=CE,
∴∠ECA=∠DCA=60°,
∴∠ECO=∠ECA+∠OCA=60°+30°=90°,
∴EF为⊙O的切线.
点评 本题考查了切线的判定、轴对称的性质、等腰三角形的判定、等边三角形的判定与性质,灵活运用相关的性质定理是解题的关键.


 第1卷单元月考期中期末系列答案
第1卷单元月考期中期末系列答案科目:初中数学 来源: 题型:解答题
 如图,在直角梯形ABCD中,AD∥BC,∠B=90°,AB=3cm,AD=14cm,BC=10cm,动点P从D点出发,沿DA方向以2cm/秒的速度运动,运动时间为t秒.
如图,在直角梯形ABCD中,AD∥BC,∠B=90°,AB=3cm,AD=14cm,BC=10cm,动点P从D点出发,沿DA方向以2cm/秒的速度运动,运动时间为t秒.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 某兴趣小组用高为1.2米的仪器测量建筑物CD的高度.如示意图,由距CD一定距离的A处用仪器观察建筑物顶部D的仰角为β,在A和C之间选一点B,由B处用仪器观察建筑物顶部D的仰角为α.测得A,B之间的距离为4米,tanα=1.6,tanβ=1.2,试求建筑物CD的高度.
某兴趣小组用高为1.2米的仪器测量建筑物CD的高度.如示意图,由距CD一定距离的A处用仪器观察建筑物顶部D的仰角为β,在A和C之间选一点B,由B处用仪器观察建筑物顶部D的仰角为α.测得A,B之间的距离为4米,tanα=1.6,tanβ=1.2,试求建筑物CD的高度.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
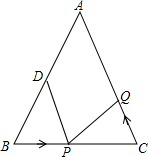 如图,在△ABC中,AB=AC=10厘米,BC=8厘米,点D为AB的中点.点P在线段BC上以3厘米/秒的速度由B点向C点运动,同时点Q在线段CA上由C点向A点运动.
如图,在△ABC中,AB=AC=10厘米,BC=8厘米,点D为AB的中点.点P在线段BC上以3厘米/秒的速度由B点向C点运动,同时点Q在线段CA上由C点向A点运动.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
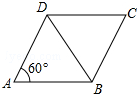 如图,已知菱形ABCD的边长为2,∠DAB=60°,则对角线AC的长是( )
如图,已知菱形ABCD的边长为2,∠DAB=60°,则对角线AC的长是( )| A. | 1 | B. | $\sqrt{3}$ | C. | 2 | D. | 2$\sqrt{3}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
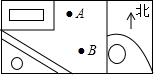 某校平面图的一部分如图所示,则对点A、B的方位的说法基本正确的是( )
某校平面图的一部分如图所示,则对点A、B的方位的说法基本正确的是( )| A. | 点A在点B的北偏西30°方向 | B. | 点A在点B的东南方向 | ||
| C. | 点A在点B的西北方向 | D. | 点A在点B的南偏东30°方向 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com