
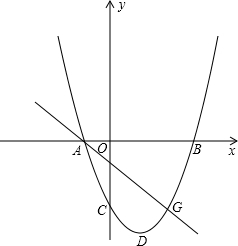
 xжсНЛгкAЁЂBСНЕуЃЌЦфжаBЕуЕФзјБъЮЊЃЈ3ЃЌ0ЃЉЃЌЧвOB=OCЃЎ
xжсНЛгкAЁЂBСНЕуЃЌЦфжаBЕуЕФзјБъЮЊЃЈ3ЃЌ0ЃЉЃЌЧвOB=OCЃЎ
|
|

|
|
| 1 |
| 2 |
| 1 |
| 2 |
| 3 |
| 2 |
| 3 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 15 |
| 4 |
| 27 |
| 8 |
| 1 |
| 2 |
| 15 |
| 4 |
| 1 |
| 2 |
| 15 |
| 4 |
| 27 |
| 8 |

| 5 |
| 5 |
| 5 |
| 5 |
| 5 |
| 5 |
| 5 |
| 5 |
| 5 |
| 5 |
| 5 |
| 5 |
| 1 |
| 2 |
| 1 |
| 2 |
| 5 |
| 5 |
| 5 |
| 5 |
| 5 |
| 5 |
| 5 |
| 5 |



| ФъМЖ | ИпжаПЮГЬ | ФъМЖ | ГѕжаПЮГЬ |
| ИпвЛ | ИпвЛУтЗбПЮГЬЭЦМіЃЁ | ГѕвЛ | ГѕвЛУтЗбПЮГЬЭЦМіЃЁ |
| ИпЖў | ИпЖўУтЗбПЮГЬЭЦМіЃЁ | ГѕЖў | ГѕЖўУтЗбПЮГЬЭЦМіЃЁ |
| ИпШ§ | ИпШ§УтЗбПЮГЬЭЦМіЃЁ | ГѕШ§ | ГѕШ§УтЗбПЮГЬЭЦМіЃЁ |
ПЦФПЃКГѕжаЪ§бЇ РДдДЃКВЛЯъ ЬтаЭЃКНтД№Ьт
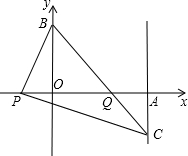 НгBPЃЌЙ§PЕузїPCЁЭPBНЛЙ§ЕуAЕФжБЯпaгкЕуCЃЈ2ЃЌyЃЉ
НгBPЃЌЙ§PЕузїPCЁЭPBНЛЙ§ЕуAЕФжБЯпaгкЕуCЃЈ2ЃЌyЃЉВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃКВЛЯъ ЬтаЭЃКЬюПеЬт
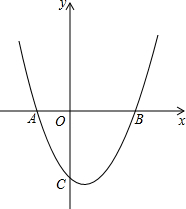
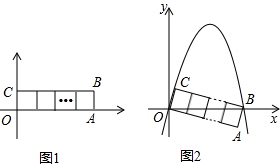 +bx+cЃЈaЃМ0ЃЉЃЌШчЙћХзЮяЯпЭЌЪБОЙ§ЕуOЁЂBЁЂCЃК
+bx+cЃЈaЃМ0ЃЉЃЌШчЙћХзЮяЯпЭЌЪБОЙ§ЕуOЁЂBЁЂCЃКВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃКВЛЯъ ЬтаЭЃКНтД№Ьт
| 1 |
| 2 |
| b |
| 2a |
| 4ac-b2 |
| 4a |
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃКВЛЯъ ЬтаЭЃКНтД№Ьт
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃКВЛЯъ ЬтаЭЃКНтД№Ьт

ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃКВЛЯъ ЬтаЭЃКНтД№Ьт
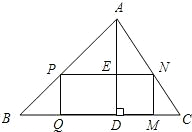 ЯТдйЦДГЩЃЈВЛМЦНгЗьгУСЯМАЫ№КФЃЉгыГЄЗНаЮPQMNДѓаЁвЛбљЕФГЄЗНаЮЃПШєФмЃЌЪдИјГівЛжжЦДЗЈЃЛШєВЛФмЃЌЪдЫЕУїРэгЩЃЎ
ЯТдйЦДГЩЃЈВЛМЦНгЗьгУСЯМАЫ№КФЃЉгыГЄЗНаЮPQMNДѓаЁвЛбљЕФГЄЗНаЮЃПШєФмЃЌЪдИјГівЛжжЦДЗЈЃЛШєВЛФмЃЌЪдЫЕУїРэгЩЃЎВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃКВЛЯъ ЬтаЭЃКНтД№Ьт
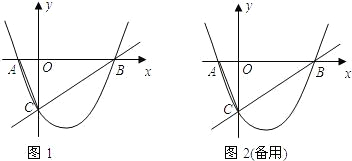
 y=x2-mx+nЃЌШєЗНГЬx2-mx+n=0СНИљЕЙЪ§КЭЮЊ-2ЃЎ
y=x2-mx+nЃЌШєЗНГЬx2-mx+n=0СНИљЕЙЪ§КЭЮЊ-2ЃЎВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃКВЛЯъ ЬтаЭЃКНтД№Ьт
| 1 |
| 2 |
| 1 |
| 2 |
ВщПДД№АИКЭНтЮі>>
АйЖШжТаХ - СЗЯАВсСаБэ - ЪдЬтСаБэ
КўББЪЁЛЅСЊЭјЮЅЗЈКЭВЛСМаХЯЂОйБЈЦНЬЈ | ЭјЩЯгаКІаХЯЂОйБЈзЈЧј | ЕчаХеЉЦОйБЈзЈЧј | ЩцРњЪЗащЮожївхгаКІаХЯЂОйБЈзЈЧј | ЩцЦѓЧжШЈОйБЈзЈЧј
ЮЅЗЈКЭВЛСМаХЯЂОйБЈЕчЛАЃК027-86699610 ОйБЈгЪЯфЃК58377363@163.com