练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    计算：（﹣2）0+（﹣1）2014+﹣sin45°；


    原式=1+1+﹣=2；

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：


    如图1，边长为4的正方形ABCD中，点E在AB边上（不与点A、B重合），点F在BC边上（不与点B、C重合）

    第一次操作：将线段EF绕点F顺时针旋转，当点E落在正方形上时，记为点G；

    第二次操作：将线段FG绕点G顺时针旋转，当点F落在正方形上时，记为点H；

    依此操作下去

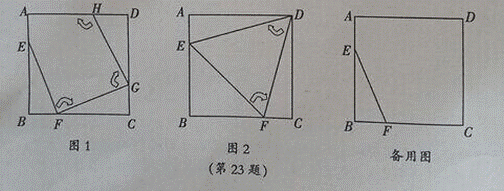
    （1）       图2中的三角形EFD是经过两次操作后得到的，其形状为_______,求此时线段EF的长；

    （2）       若经过三次操作可得到四边形EFGH的形状为_________,此时AE与BF的数量关系是_______;

    ①     请判断四边形EFGH的形状为______,此时AE与BF的数量关系是_______

    ② 以①中的结论为前提，设AE的长为x，四边形EFGH的面积为y，求y与x的函数关系式及面积y的取值范围。

    查看答案和解析>>

    科目：初中数学 来源： 题型：


    我们知道，无限循环小数都可以转化为分数．例如：将转化为分数时，可设＝x，则x＝0.3＋x，解得x＝，即＝．仿此方法，将化成分数是    ．

    查看答案和解析>>

    科目：初中数学 来源： 题型：


    不等式的解集在数轴上表示正确的是（　　）

    　

    A．

    B．

    C．

    D．

    查看答案和解析>>

    科目：初中数学 来源： 题型：


    已知P1（1，y1），P2（2，y2）是正比例函数y=x的图象上的两点，则y1　　y2（填“＞”或“＜”或“=”）．

    查看答案和解析>>

    科目：初中数学 来源： 题型：


    马小虎的家距离学校1800米，一天马小虎从家去上学，出发10分钟后，爸爸发现他的数学课本忘记拿了，立即带上课本去追他，在距离学校200米的地方追上了他，已知爸爸的速度是马小虎速度的2倍，求马小虎的速度．

    查看答案和解析>>

    科目：初中数学 来源： 题型：


    一个布袋里装有5个球，其中3个红球，2个白球，每个球除颜色外其它完全相同，从中任意摸出一个球，是红球的概率是

    A.             B.               C.             D.

    查看答案和解析>>

    科目：初中数学 来源： 题型：


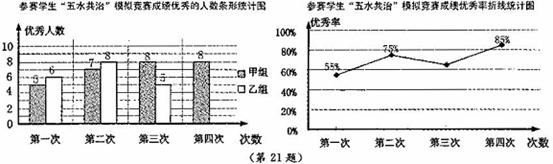
    九（3）班为了组队参加学校举行的“五水共治”知识竞赛，在班里选取了若干名学生，分成人数相同的甲乙两组，进行了四次“五水共治”模拟竞赛，成绩优秀的人数和优秀率分别绘制成如下统计图。

    根据统计图，解答下列问题：

    （1）第三次成绩的优秀率是多少？并将条形统计图补充完整；

    （2）已求得甲组成绩优秀人数的平均数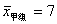，方差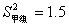，请通过计算说明，哪一组成绩优秀的人数较稳定？

    查看答案和解析>>

    科目：初中数学 来源： 题型：


    已知：如图，△ABC中，∠C=90°，点O为△ABC的三条角平分线的交点，OD⊥BC，OE⊥AC，OF⊥AB，点D、E、F分别是垂足，且AB=10，BC=8，CA=6，则点O到三边AB、AC和BC的距离分别等于（　　）

    　

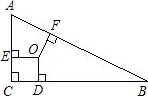
    A．

    2、2、2

    B．

    3、3、3

    C．

    4、4、4

    D．

    2、3、5

    　

    查看答案和解析>>

    同步练习册答案