
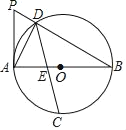
【题目】如图,AB为⊙O的直径,且AB=m(m为常数),点C为![]() 的中点,点D为圆上一动点,过A点作⊙O的切线交BD的延长线于点P,弦CD交AB于点E.
的中点,点D为圆上一动点,过A点作⊙O的切线交BD的延长线于点P,弦CD交AB于点E.
(1)当DC⊥AB时,则![]() = ;
= ;
(2)①当点D在![]() 上移动时,试探究线段DA,DB,DC之间的数量关系;并说明理由;
上移动时,试探究线段DA,DB,DC之间的数量关系;并说明理由;
②设CD长为t,求△ADB的面积S与t的函数关系式;
(3)当![]() 时,求
时,求![]() 的值.
的值.
【答案】(1)![]() ;(2)①DA+DB=
;(2)①DA+DB=![]() DC,②S=
DC,②S=![]() t2﹣
t2﹣![]() m2 ;(3)
m2 ;(3)![]() .
.
【解析】
(1)首先证明当DC⊥AB时,DC也为圆的直径,且△ADB为等腰直角三角形,即可求出结果;
(2)①分别过点A,B作CD的垂线,连接AC,BC,分别构造△ADM和△BDN两个等腰直角三形及△NBC和△MCA两个全等的三角形,容易证出线段DA,DB,DC之间的数量关系;
②通过完全平方公式(DA+DB)2=DA2+DB2+2DADB的变形及将已知条件AB=m代入即可求出结果;
(3)通过设特殊值法,设出PD的长度,再通过相似及面积法求出相关线段的长度,即可求出结果.
解:(1)如图1,∵AB为⊙O的直径,
∴∠ADB=90°,
∵C为![]() 的中点,
的中点,
∴![]() ,
,
∴∠ADC=∠BDC=45°,
∵DC⊥AB,
∴∠DEA=∠DEB=90°,
∴∠DAE=∠DBE=45°,
∴AE=BE,
∴点E与点O重合,
∴DC为⊙O的直径,
∴DC=AB,
在等腰直角三角形DAB中,
DA=DB=![]() AB,
AB,
∴DA+DB=![]() AB=
AB=![]() CD,
CD,
∴![]() =
=![]() ;
;

(2)①如图2,过点A作AM⊥DC于M,过点B作BN⊥CD于N,连接AC,BC,
由(1)知![]() ,
,
∴AC=BC,
∵AB为⊙O的直径,
∴∠ACB=∠BNC=∠CMA=90°,
∴∠NBC+∠BCN=90°,∠BCN+∠MCA=90°,
∴∠NBC=∠MCA,
在△NBC和△MCA中,
 ,
,
∴△NBC≌△MCA(AAS),
∴CN=AM,
由(1)知∠DAE=∠DBE=45°,
AM=![]() DA,DN=
DA,DN=![]() DB,
DB,
∴DC=DN+NC=![]() DB+
DB+![]() DA=
DA=![]() (DB+DA),
(DB+DA),
即DA+DB=![]() DC;
DC;

②在Rt△DAB中,
DA2+DB2=AB2=m2,
∵(DA+DB)2=DA2+DB2+2DADB,
且由①知DA+DB=![]() DC=
DC=![]() t,
t,
∴(![]() t)2=m2+2DADB,
t)2=m2+2DADB,
∴DADB=t2﹣![]() m2,
m2,
∴S△ADB=![]() DADB=
DADB=![]() t2﹣
t2﹣![]() m2,
m2,
∴△ADB的面积S与t的函数关系式S=![]() t2﹣
t2﹣![]() m2;
m2;
(3)如图3,过点E作EH⊥AD于H,EG⊥DB于G,
则NE=ME,四边形DHEG为正方形,
由(1)知![]() ,
,
∴AC=BC,
∴△ACB为等腰直角三角形,
∴AB=![]() AC,
AC,
∵![]() ,
,
设PD=9![]() ,则AC=20,AB=20
,则AC=20,AB=20![]() ,
,
∵∠DBA=∠DBA,∠PAB=∠ADB,
∴△ABD∽△PBA,
∴![]() ,
,
∴![]() ,
,
∴DB=16![]() ,
,
∴AD=![]() =12
=12![]() ,
,
设NE=ME=x,
∵S△ABD=![]() ADBD=
ADBD=![]() ADNE+
ADNE+![]() BDME,
BDME,
∴![]() ×12
×12![]() ×16
×16![]() =
=![]() ×12
×12![]() x+
x+![]() ×16
×16![]() x,
x,
∴x=![]() ,
,
∴DE=![]() HE=
HE=![]() x=
x=![]() ,
,
又∵AO=![]() AB=10
AB=10![]() ,
,
∴![]() .
.



 同步奥数系列答案
同步奥数系列答案科目:初中数学 来源: 题型:
【题目】已知关于x的方程x2-(a+b)x+ab-1=0,x1、x2是此方程的两个实数根,现给出三个结论:①x1≠x2;②x1x2<ab;③![]() +
+![]() <a2+b2.则正确结论的序号是______.(填上你认为正确的所有序号)
<a2+b2.则正确结论的序号是______.(填上你认为正确的所有序号)
查看答案和解析>>
科目:初中数学 来源: 题型:
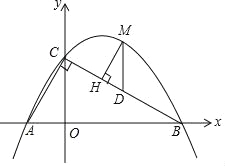
【题目】如图,直线y=﹣![]() x+
x+![]() 分别与x轴、y轴交于B、C两点,点A在x轴上,∠ACB=90°,抛物线y=ax2+bx+
分别与x轴、y轴交于B、C两点,点A在x轴上,∠ACB=90°,抛物线y=ax2+bx+![]() 经过A,B两点.
经过A,B两点.
(1)求A、B两点的坐标;
(2)求抛物线的解析式;
(3)点M是直线BC上方抛物线上的一点,过点M作MH⊥BC于点H,作MD∥y轴交BC于点D,求△DMH周长的最大值.
查看答案和解析>>
科目:初中数学 来源: 题型:
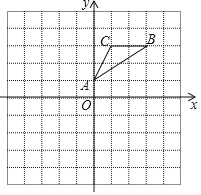
【题目】如图,△ABC的顶点坐标分别为A(0,1),B(3,3),C(1,3).
(1)画出△ABC关于点O的中心对称图形△A1B1C1;
(2)画出△ABC绕点A逆时针旋转90°的△AB2C2;直接写出点C2的坐标为 ;
(3)求在△ABC旋转到△AB2C2的过程中,点C所经过的路径长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某饭店推出一种早点套餐,试销一段时间后发现,每份套餐的成本为5元,若每份售价不超过10元,每天可销售400份;若每份售价超过10元,每提高1元,每天的销售量就减少40份,该店每天固定支出费用为600元![]() 不含套餐成本
不含套餐成本![]() 为了便于结算,每份套餐的售价取整数,设每份套餐的售价为
为了便于结算,每份套餐的售价取整数,设每份套餐的售价为![]() 元,该店日销售利润为y元
元,该店日销售利润为y元![]() 日销售利润
日销售利润![]() 每天的销售额
每天的销售额![]() 套餐成本
套餐成本![]() 每天固定支出
每天固定支出![]()
![]() 求y与x的函数关系式并写出自变量的取值范围.
求y与x的函数关系式并写出自变量的取值范围.
![]() 该店要想获得最大日销售利润,又要吸引顾客,使每天销售量较大,按此要求,每份套餐的售价应定为多少元?此时日销售利润为多少元?
该店要想获得最大日销售利润,又要吸引顾客,使每天销售量较大,按此要求,每份套餐的售价应定为多少元?此时日销售利润为多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
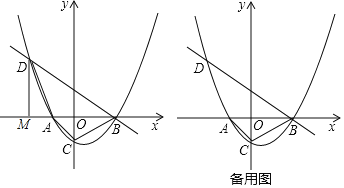
【题目】如图,已知抛物线![]() (k为常数,且
(k为常数,且![]() )与x轴从左至右依次交于A,B两点,与y轴交于点C过点B的直线
)与x轴从左至右依次交于A,B两点,与y轴交于点C过点B的直线![]() 与抛物线的另一交点为D.
与抛物线的另一交点为D.
![]() 若点D的横坐标为
若点D的横坐标为![]() ,求抛物线的函数表达式;
,求抛物线的函数表达式;
![]() 过D点向x轴作垂线,垂足为点M,连结AD,若
过D点向x轴作垂线,垂足为点M,连结AD,若![]() ,求点D的坐标;
,求点D的坐标;
![]() 若在第一象限的抛物线上有一点P,使得以点A,B,P为顶点的三角形与
若在第一象限的抛物线上有一点P,使得以点A,B,P为顶点的三角形与![]() 相似,请直接写出
相似,请直接写出![]() 的面积.
的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一个透明的布袋里装有2个红球,![]() 个白球,它们除颜色外其余都相同,已知任意摸出1个球是红球的概率为
个白球,它们除颜色外其余都相同,已知任意摸出1个球是红球的概率为![]() .
.
(1)求![]() 的值;
的值;
(2)先任意摸出1个球,记下颜色后不放回,搅匀,再摸出一个球,请利用画树状图或列表的方法求出连续两次都摸出红球的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
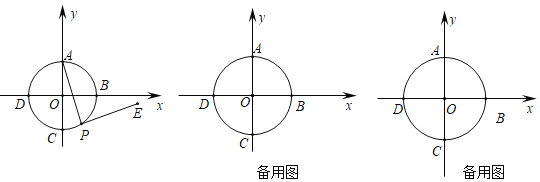
【题目】如图,半径为4且以坐标原点为圆心的圆O交x轴,y轴于点B、D、A、C,过圆上的动点![]() 不与A重合
不与A重合![]() 作
作![]() ,且
,且![]() 在AP右侧
在AP右侧![]() .
.
![]() 当P与C重合时,求出E点坐标;
当P与C重合时,求出E点坐标;
![]() 连接PC,当
连接PC,当![]() 时,求点P的坐标;
时,求点P的坐标;
![]() 连接OE,直接写出线段OE的取值范围.
连接OE,直接写出线段OE的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com