
 如图,已知抛物线y=-$\frac{1}{2}$x2+bx+c与坐标轴分别交于点A(0,8)、B(8,0)和点E,动点C从原点O开始沿OA方向以每秒1个单位长度移动,动点D从点B开始沿BO方向以每秒1个单位长度移动,动点C、D同时出发,当动点D到达原点O时,点C、D停止运动.
如图,已知抛物线y=-$\frac{1}{2}$x2+bx+c与坐标轴分别交于点A(0,8)、B(8,0)和点E,动点C从原点O开始沿OA方向以每秒1个单位长度移动,动点D从点B开始沿BO方向以每秒1个单位长度移动,动点C、D同时出发,当动点D到达原点O时,点C、D停止运动.分析 (1)将点A(0,8)、B(8,0)代入抛物线y=-$\frac{1}{2}$x2+bx+c即可求出抛物线的解析式为:y=-$\frac{1}{2}$x2+3x+8;
(2)根据题意得:当D点运动t秒时,BD=t,OC=t,然后由点A(0,8)、B(8,0),可得OA=8,OB=8,从而可得OD=8-t,然后令y=0,求出点E的坐标为(-2,0),进而可得OE=2,DE=2+8-t=10-t,然后利用三角形的面积公式即可求△CED的面积S与D点运动时间t的函数解析式为:S=-$\frac{1}{2}$t2+5t,然后转化为顶点式即可求出最值为:S最大=$\frac{25}{2}$;
(3)由(2)知:当t=5时,S最大=$\frac{25}{2}$,进而可知:当t=5时,OC=5,OD=3,进而可得CD=$\sqrt{34}$,从而确定C(0,5),D(3,0)然后根据待定系数法求出直线CD的解析式为:y=-$\frac{5}{3}$x+5,然后过E点作EF∥CD,交抛物线与点P,然后求出直线EF的解析式,与抛物线联立方程组解得即可得到其中的一个点P的坐标,然后利用面积法求出点E到CD的距离为:$\frac{25\sqrt{34}}{34}$,然后过点D作DN⊥CD,垂足为N,且使DN=$\frac{25\sqrt{34}}{34}$,然后求出N的坐标,然后过点N作NH∥CD,与抛物线交与点P,然后求出直线NH的解析式,与抛物线联立方程组求解即可得到其中的另两个点P的坐标.
解答 解:(1)将点A(0,8)、B(8,0)代入抛物线y=-$\frac{1}{2}$x2+bx+c得:$\left\{\begin{array}{l}{c=8}\\{-\frac{1}{2}×64+8b+c=0}\end{array}\right.$,
解得:b=3,c=8,
∴抛物线的解析式为:y=-$\frac{1}{2}$x2+3x+8,
故答案为:y=-$\frac{1}{2}$x2+3x+8;
(2)∵点A(0,8)、B(8,0),
∴OA=8,OB=8,
令y=0,得:-$\frac{1}{2}$x2+3x+8=0,
解得:x1=8,x2=-2,
∵点E在x轴的负半轴上,
∴点E(-2,0),
∴OE=2,
根据题意得:当D点运动t秒时,BD=t,OC=t,
∴OD=8-t,
∴DE=OE+OD=10-t,
∴S=$\frac{1}{2}$•DE•OC=$\frac{1}{2}$•(10-t)•t=-$\frac{1}{2}$t2+5t,
即S=-$\frac{1}{2}$t2+5t=-$\frac{1}{2}$(t-5)2+$\frac{25}{2}$,
∴当t=5时,S最大=$\frac{25}{2}$;
(3)方法一:
由(2)知:当t=5时,S最大=$\frac{25}{2}$,
∴当t=5时,OC=5,OD=3,
∴C(0,5),D(3,0),
由勾股定理得:CD=$\sqrt{34}$,
设直线CD的解析式为:y=kx+b,
将C(0,5),D(3,0),代入上式得:
k=-$\frac{5}{3}$,b=5,
∴直线CD的解析式为:y=-$\frac{5}{3}$x+5,
过E点作EF∥CD,交抛物线与点P,如图1,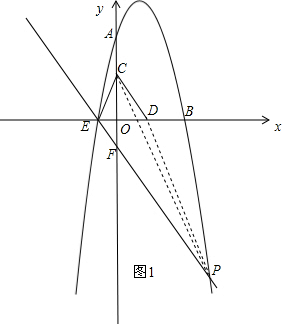
设直线EF的解析式为:y=-$\frac{5}{3}$x+b,
将E(-2,0)代入得:b=-$\frac{10}{3}$,
∴直线EF的解析式为:y=-$\frac{5}{3}$x-$\frac{10}{3}$,
将y=-$\frac{5}{3}$x-$\frac{10}{3}$,与y=-$\frac{1}{2}$x2+3x+8联立成方程组得:
$\left\{\begin{array}{l}{y=-\frac{5}{3}x-\frac{10}{3}}\\{y=-\frac{1}{2}{x}^{2}+3x+8}\end{array}\right.$,
解得:$\left\{\begin{array}{l}{{x}_{1}=-2}\\{{y}_{1}=0}\end{array}\right.$,$\left\{\begin{array}{l}{{x}_{2}=\frac{34}{3}}\\{{y}_{2}=-\frac{200}{9}}\end{array}\right.$,
∴P($\frac{34}{3}$,-$\frac{200}{9}$);
过点E作EG⊥CD,垂足为G,
∵当t=5时,S△ECD=$\frac{1}{2}•CD•EG$=$\frac{25}{2}$,
∴EG=$\frac{25\sqrt{34}}{34}$,
过点D作DN⊥CD,垂足为N,且使DN=$\frac{25\sqrt{34}}{34}$,过点N作NM⊥x轴,垂足为M,如图2,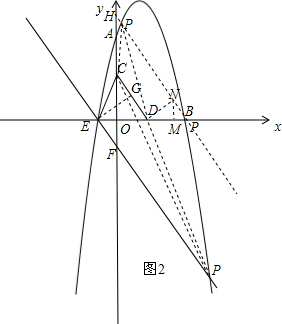
可得△EGD∽△DMN,
∴$\frac{EG}{DM}=\frac{ED}{DN}$,
即:$\frac{\frac{25\sqrt{34}}{34}}{DM}=\frac{5}{\frac{25\sqrt{34}}{34}}$,
解得:DM=$\frac{125}{34}$,
∴OM=$\frac{227}{34}$,
由勾股定理得:MN=$\sqrt{D{N}^{2}-D{M}^{2}}$=$\frac{75}{34}$,
∴N($\frac{227}{34}$,$\frac{75}{34}$),
过点N作NH∥CD,与抛物线交与点P,如图2,
设直线NH的解析式为:y=-$\frac{5}{3}$x+b,
将N($\frac{227}{34}$,$\frac{75}{34}$),代入上式得:b=$\frac{40}{3}$,
∴直线NH的解析式为:y=-$\frac{5}{3}$x+$\frac{40}{3}$,
将y=-$\frac{5}{3}$x+$\frac{40}{3}$,与y=-$\frac{1}{2}$x2+3x+8联立成方程组得:
$\left\{\begin{array}{l}{y=-\frac{5}{3}x+\frac{40}{3}}\\{y=-\frac{1}{2}{x}^{2}+3x+8}\end{array}\right.$,
解得:$\left\{\begin{array}{l}{{x}_{1}=8}\\{{y}_{1}=0}\end{array}\right.$,$\left\{\begin{array}{l}{{x}_{2}=\frac{4}{3}}\\{{y}_{2}=\frac{100}{9}}\end{array}\right.$,
∴P(8,0)或P($\frac{4}{3}$,$\frac{100}{9}$),
综上所述:当△CED的面积最大时,在抛物线上存在点P(点E除外),使△PCD的面积等于△CED的最大面积,点P的坐标为:P($\frac{34}{3}$,-$\frac{200}{9}$)或P(8,0)或P($\frac{4}{3}$,$\frac{100}{9}$).
方法二:
由(2)知,C(0,5),D(3,0),∴lCD:y=-$\frac{5}{3}$x+5,
作PH⊥x轴,交CD于点H,
∵P在抛物线上,∴设P(6m,-18m2+18m+8),
∴H(6m,-10m+5),C(0,5),D(3,0),
S△PCD=$\frac{1}{2}$|(DX-CX)(PY-HY)|,
∵S△CED=$\frac{25}{2}$,
∴$\frac{3}{2}×|-10m+5+18{m}^{2}-18m-8|=\frac{25}{2}$,
∴3×|18m2-28m-3|=25,
①3×(18m2-28m-3)=25,
∴m1=-$\frac{1}{3}$,m2=$\frac{17}{9}$,
∴6m1=-2(舍),6m2=$\frac{34}{3}$,
②3×(18m2-28m-3)=-25,
∴m1=$\frac{4}{3}$,m2=$\frac{2}{9}$,
∴6m1=8,6m2=$\frac{4}{3}$,
综上所述,点P的坐标为:P($\frac{34}{3}$,-$\frac{200}{9}$)或P(8,0)或P($\frac{4}{3}$,$\frac{100}{9}$).
点评 此题考查了二次函数的综合题,主要涉及了以下知识点:用待定系数法求函数关系式,函数的最值问题,三角形的面积公式及用二元一次方程组求交点问题等.解决(3)用到的知识点是两条平行线间的距离处处相等.


 小学课时特训系列答案
小学课时特训系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,在一笔直的海岸线l上有A、B两个码头,A在B的正东方向,一艘小船从A码头沿它的北偏西60°的方向行驶了20海里到达点P处,此时从B码头测得小船在它的北偏东45°的方向.求此时小船到B码头的距离(即BP的长)和A、B两个码头间的距离(结果都保留根号).
如图,在一笔直的海岸线l上有A、B两个码头,A在B的正东方向,一艘小船从A码头沿它的北偏西60°的方向行驶了20海里到达点P处,此时从B码头测得小船在它的北偏东45°的方向.求此时小船到B码头的距离(即BP的长)和A、B两个码头间的距离(结果都保留根号).查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 现有甲、乙两个容器,分别装有进水管和出水管,两容器的进出水速度不变,先打开乙容器的进水管,2分钟时再打开甲容器的进水管,又过2分钟关闭甲容器的进水管,再过4分钟同时打开甲容器的进、出水管.直到12分钟时,同时关闭两容器的进出水管.打开和关闭水管的时间忽略不计.容器中的水量y(升)与乙容器注水时间x(分)之间的关系如图所示.
现有甲、乙两个容器,分别装有进水管和出水管,两容器的进出水速度不变,先打开乙容器的进水管,2分钟时再打开甲容器的进水管,又过2分钟关闭甲容器的进水管,再过4分钟同时打开甲容器的进、出水管.直到12分钟时,同时关闭两容器的进出水管.打开和关闭水管的时间忽略不计.容器中的水量y(升)与乙容器注水时间x(分)之间的关系如图所示.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
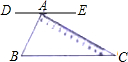 如图,一块含30°角的直角三角板ABC的直角顶点A在直线DE上,且BC∥DE,则∠CAE等于( )
如图,一块含30°角的直角三角板ABC的直角顶点A在直线DE上,且BC∥DE,则∠CAE等于( )| A. | 30° | B. | 45° | C. | 60° | D. | 90° |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com