
【题目】如图,在△ABC中,∠ABC=∠ACB,以AC为直径的⊙O分别交AB、BC于点M、N,点P在AB的延长线上,且∠CAB=2∠BCP.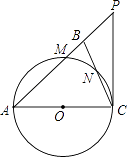
(1)求证:直线CP是⊙O的切线;
(2)若BC=2 ![]() ,sin∠BCP=
,sin∠BCP= ![]() ,求⊙O的半径及△ACP的周长.
,求⊙O的半径及△ACP的周长.
【答案】
(1)证明:连接AN,
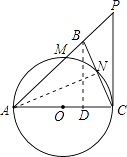
∵∠ABC=∠ACB,∴AB=AC,
∵AC是⊙O的直径,∴AN⊥BC,
∴∠CAN=∠BAN,BN=CN,
∵∠CAB=2∠BCP,
∴∠CAN=∠BCP.
∵∠CAN+∠ACN=90°,
∴∠BCP+∠ACN=90°,
∴CP⊥AC
∵OC是⊙O的半径
∴CP是⊙O的切线
(2)解:∵∠ANC=90°,sin∠BCP= ![]() ,
,
∴ ![]() =
= ![]() ,
,
∴AC=5,
∴⊙O的半径为 ![]()
如图,过点B作BD⊥AC于点D.
由(1)得BN=CN= ![]() BC=
BC= ![]() ,
,
在Rt△CAN中,AN= ![]() =2
=2 ![]()
在△CAN和△CBD中,
∠ANC=∠BDC=90°,∠ACN=∠BCD,
∴△CAN∽△CBD,
∴ ![]() =
= ![]() ,
,
∴BD=4.
在Rt△BCD中,CD= ![]() =2,
=2,
∴AD=AC﹣CD=5﹣2=3,
∵BD∥CP,
∴ ![]() =
= ![]() ,
, ![]() =
= ![]()
∴CP= ![]() ,BP=
,BP= ![]()
∴△APC的周长是AC+PC+AP=20.
【解析】(1)由等角对等边得AB=AC,连接AN,由圆周角定理及等角三角形的三线合一得出∠CAN=∠BCP.根据直角三角形两锐角互余及等量代换得出∠BCP+∠ACN=90°,得出结论;(2)根据锐角三角函数的定义,找到圆的半径,在Rt△CAN中根据勾股定理得出AN,进而判断出△CAN∽△CBD,根据相似三角形对应边成比例得出BD的长度,在Rt△BCD中由勾股定理得出CD,再由平行线分线段成比例得出CP,BP的长度。
【考点精析】利用等腰三角形的性质和勾股定理的概念对题目进行判断即可得到答案,需要熟知等腰三角形的两个底角相等(简称:等边对等角);直角三角形两直角边a、b的平方和等于斜边c的平方,即;a2+b2=c2.


科目:初中数学 来源: 题型:
【题目】解方程组:①![]() ②
②![]() ③
③![]() ④
④![]() ,比较适宜的方法是( )
,比较适宜的方法是( )
A.①②用代入法,③④用加减法B.①③用代入法,②④用加减法
C.②③用代入法,①④用加减法D.②④用代入法,①③用加减法
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下面是小芸设计的“作三角形一边上的高”的尺规作图过程.
已知:△ABC.
求作:△ABC的边BC上的高AD.
作法:①以点A为圆心,适当长为半径画弧,
交直线BC于点M,N;
②分别以点M,N为圆心,以大于![]() MN的长为半径画弧,两弧相交于点P;
MN的长为半径画弧,两弧相交于点P;
③作直线AP交BC于点D,则线段AD即为所求△ABC的边BC上的高.
根据小芸设计的尺规作图过程,
(1)使用直尺和圆规,补全图形;(保留作图痕迹)
(2)完成下面的证明:
证明:∵AM= ,MP= ,
∴AP是线段MN的垂直平分线.( )(填推理的依据)
∴AD⊥BC于D,即线段AD为△ABC的边BC上的高.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,直线a 、b被直线c所截,现给出下列四种条件:
①∠2=∠6 ②∠2=∠8 ③∠1+∠4=180° ④∠3=∠8,其中能判断是a∥b的条件的序号是( )

A. ①② B. ①③ C. ①④ D. ③④
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一般情况下,![]() 不成立,但有些数可以使得它成立,例如:a=1,b=2.我们称使得
不成立,但有些数可以使得它成立,例如:a=1,b=2.我们称使得![]() 成立的一对数a,b为“相伴数对”,记为(a,b).
成立的一对数a,b为“相伴数对”,记为(a,b).
(1)判断数对(﹣2,1),(3,3)是否是“相伴数对”;
(2)若(k,﹣1)是“相伴数对”,求k的值;
(3)若(4,m)是“相伴数对”,求代数式![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(10分)如图,已知△ABC为等边三角形,点D、E分别在BC、AC边上,且AE=CD,AD与BE相交于点F。

(1)求证:△ABE≌△CAD;(2)求∠BFD的度数。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】△ABC与△A′B′C′在平面直角坐标系中的位置如图.
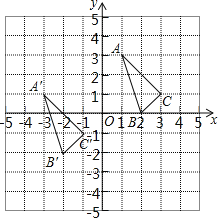
(1)分别写出下列各点的坐标: A′ ;B′ ;C′ ;
(2)若点P(a,b)是△ABC内部一点,则平移后△A′B′C′内的对应点P′的坐标为 ;
(3)求△ABC的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】五一期间,小明和小颖相约到乐山大佛景区参观.小明乘私家车从成都出发1小时后,小颖乘坐高铁从成都出发,先到乐山高铁站,然后转乘出租车到乐山大佛景区(换车时间忽略不计),两人恰好同时到达景区.他们离开成都的距离y(千米)与时间t(小时)的关系如图所示,请结合图象解决下面问题.
(1)高铁的平均速度是每小时多少千米?
(2)当小颖到达乐山高铁站时,小明距离乐山大佛景区还有多少千米?

查看答案和解析>>
科目:初中数学 来源: 题型:
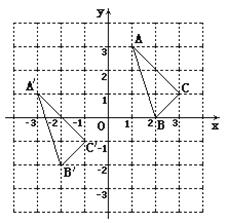
【题目】△ A B C与![]() 在平面直角坐标系中的位置如图.
在平面直角坐标系中的位置如图.
(1)分别写出下列各点的坐标: ![]() ______ ;
______ ; ![]() _______ ;
_______ ; ![]() _______ ;
_______ ;
(2)说明![]() 由△ A B C经过怎样的平移得到? ________________________________.
由△ A B C经过怎样的平移得到? ________________________________.
(3)若点![]() (
(![]() ,
, ![]() )是△ A B C内部一点,则平移后
)是△ A B C内部一点,则平移后![]() 内的对应点
内的对应点![]() 的坐标为 ________ ;
的坐标为 ________ ;
(4)求△ A B C的面积..
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com