
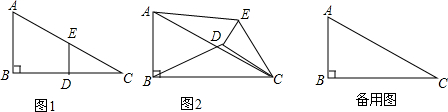
分析 (1)①当α=0°时,在Rt△ABC中,由勾股定理,求出AC的值是多少;然后根据点D、E分别是边BC、AC的中点,分别求出AE、BD的大小,即可求出$\frac{AE}{BD}$的值是多少.
②α=180°时,可得AB∥DE,然后根据$\frac{AC}{AE}=\frac{BC}{BD}$,求出$\frac{AE}{BD}$的值是多少即可.
(2)首先判断出∠ECA=∠DCB,再根据$\frac{EC}{DC}=\frac{AC}{BC}=\frac{\sqrt{5}}{2}$,判断出△ECA∽△DCB,即可求出$\frac{AE}{BD}$的值是多少,进而判断出$\frac{AE}{BD}$的大小没有变化即可.
(3)根据题意,分两种情况:①点A,D,E所在的直线和BC平行时;②点A,D,E所在的直线和BC相交时;然后分类讨论,求出线段BD的长各是多少即可.
解答 解:(1)①当α=0°时,
∵Rt△ABC中,∠B=90°,
∴AC=$\sqrt{{AB}^{2}{+BC}^{2}}=\sqrt{{(8÷2)}^{2}{+8}^{2}}=4\sqrt{5}$,
∵点D、E分别是边BC、AC的中点,
∴$AE=4\sqrt{5}÷2=2\sqrt{5},BD=8÷2=4$,
∴$\frac{AE}{BD}=\frac{2\sqrt{5}}{4}=\frac{\sqrt{5}}{2}$.
②如图1, ,
,
当α=180°时,
可得AB∥DE,
∵$\frac{AC}{AE}=\frac{BC}{BD}$,
∴$\frac{AE}{BD}=\frac{AC}{BC}$=$\frac{4\sqrt{5}}{8}=\frac{\sqrt{5}}{2}$.
故答案为:$\frac{\sqrt{5}}{2}、\frac{\sqrt{5}}{2}$.
(2)如图2,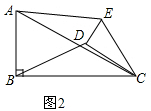 ,
,
当0°≤α<360°时,$\frac{AE}{BD}$的大小没有变化,
∵∠ECD=∠ACB,
∴∠ECA=∠DCB,
又∵$\frac{EC}{DC}=\frac{AC}{BC}=\frac{\sqrt{5}}{2}$,
∴△ECA∽△DCB,
∴$\frac{AE}{BD}=\frac{EC}{DC}=\frac{\sqrt{5}}{2}$.
(3)①如图3,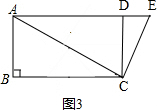 ,
,
∵AC=4$\sqrt{5}$,CD=4,CD⊥AD,
∴AD=$\sqrt{{AC}^{2}{-CD}^{2}}$=$\sqrt{{(4\sqrt{5})}^{2}{-4}^{2}}=\sqrt{80-16}=8$,
∵AD=BC,AB=DC,∠B=90°,
∴四边形ABCD是矩形,
∴$BD=AC=4\sqrt{5}$.
②如图4,连接BD,过点D作AC的垂线交AC于点Q,过点B作AC的垂线交AC于点P,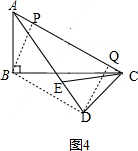 ,
,
∵AC=4$\sqrt{5}$,CD=4,CD⊥AD,
∴AD=$\sqrt{{AC}^{2}{-CD}^{2}}$=$\sqrt{{(4\sqrt{5})}^{2}{-4}^{2}}=\sqrt{80-16}=8$,
∵点D、E分别是边BC、AC的中点,
∴DE=$\frac{1}{2}AB=\frac{1}{2}×(8÷2)=\frac{1}{2}×4$=2,
∴AE=AD-DE=8-2=6,
由(2),可得
$\frac{AE}{BD}=\frac{\sqrt{5}}{2}$,
∴BD=$\frac{6}{\frac{\sqrt{5}}{2}}$=$\frac{12\sqrt{5}}{5}$.
综上所述,BD的长为4$\sqrt{5}$或$\frac{12\sqrt{5}}{5}$.
点评 (1)此题主要考查了几何变换综合题,考查了分析推理能力,考查了分类讨论思想的应用,考查了数形结合思想的应用,要熟练掌握.
(2)此题还考查了相似三角形、全等三角形的判定和性质的应用,要熟练掌握.
(3)此题还考查了线段长度的求法,以及矩形的判定和性质的应用,要熟练掌握.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:解答题
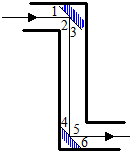 如图所示,潜望镜的两个镜子是平行放置的,光线经过镜子反射后,有∠1=∠3,∠4=∠6,请你解释为什么进入潜望镜的光线和离开潜望镜的光线也是平行的?
如图所示,潜望镜的两个镜子是平行放置的,光线经过镜子反射后,有∠1=∠3,∠4=∠6,请你解释为什么进入潜望镜的光线和离开潜望镜的光线也是平行的?查看答案和解析>>
科目:初中数学 来源: 题型:填空题
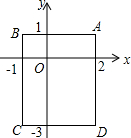 如图,在平面直角坐标系xoy中,已知点A(2,1)、B(-1,1)、C(-1,-3)、D(2,-3),把一根长为2015个单位长度没有弹性的细线(线的粗细忽略不计)的一端固定在D处,并按D→C→B→A→D…的规律紧绕在四边形ABCD的边上,则细线的另一端所在位置的点的坐标为(2,-2).
如图,在平面直角坐标系xoy中,已知点A(2,1)、B(-1,1)、C(-1,-3)、D(2,-3),把一根长为2015个单位长度没有弹性的细线(线的粗细忽略不计)的一端固定在D处,并按D→C→B→A→D…的规律紧绕在四边形ABCD的边上,则细线的另一端所在位置的点的坐标为(2,-2).查看答案和解析>>
科目:初中数学 来源: 题型:填空题
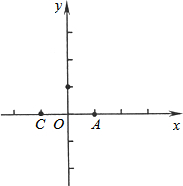 在平面直角坐标系中,点A,B,C的坐标分别为(1,0),(0,1),(-1,0).一个电动玩具从坐标原点O出发,第一次跳跃到点P1,使得点P1与点O关于点A成中心对称;第二次跳跃到点P2,使得点P2与点P1关于点B成中心对称;第三次跳跃到点P3,使得点P3与点P2关于点C成中心对称;第四次跳跃到点P4,使得点P4与点P3关于点A成中心对称;第五次跳跃到点P5,使得点P5与点P4关于点B成中心对称;…照此规律重复下去.则点P3的坐标为(0,-2);点Pn在y轴上,则点Pn的坐标为(0,0)或(0,-2).
在平面直角坐标系中,点A,B,C的坐标分别为(1,0),(0,1),(-1,0).一个电动玩具从坐标原点O出发,第一次跳跃到点P1,使得点P1与点O关于点A成中心对称;第二次跳跃到点P2,使得点P2与点P1关于点B成中心对称;第三次跳跃到点P3,使得点P3与点P2关于点C成中心对称;第四次跳跃到点P4,使得点P4与点P3关于点A成中心对称;第五次跳跃到点P5,使得点P5与点P4关于点B成中心对称;…照此规律重复下去.则点P3的坐标为(0,-2);点Pn在y轴上,则点Pn的坐标为(0,0)或(0,-2).查看答案和解析>>
科目:初中数学 来源: 题型:选择题
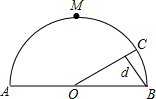 如图是自行车骑行训练场地的一部分,半圆O的直径AB=100,在半圆弧上有一运动员C从B点沿半圆周匀速运动到M(最高点),此时由于自行车故障原地停留了一段时间,修理好继续以相同的速度运动到A点停止.设运动时间为t,点B到直线OC的距离为d,则下列图象能大致刻画d与t之间的关系是( )
如图是自行车骑行训练场地的一部分,半圆O的直径AB=100,在半圆弧上有一运动员C从B点沿半圆周匀速运动到M(最高点),此时由于自行车故障原地停留了一段时间,修理好继续以相同的速度运动到A点停止.设运动时间为t,点B到直线OC的距离为d,则下列图象能大致刻画d与t之间的关系是( )| A. | 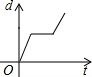 | B. | 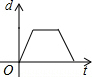 | C. | 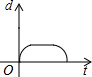 | D. | 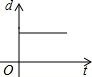 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
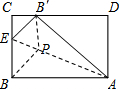 如图所示,矩形纸片ABCD中,AB=5,AD=4,将纸片折叠,使点D落在边CB上的D′处,折痕为AE,在折痕AE上存在一点P到边CB的距离与到点D的距离相等,则此相等距离为2.5.
如图所示,矩形纸片ABCD中,AB=5,AD=4,将纸片折叠,使点D落在边CB上的D′处,折痕为AE,在折痕AE上存在一点P到边CB的距离与到点D的距离相等,则此相等距离为2.5.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,在?ABCD中,对角线AC、BD相交于点O,点E、F是AD上的点,且AE=EF=FD.连接BE、BF,使它们分别与AO相交于点G、H.
如图,在?ABCD中,对角线AC、BD相交于点O,点E、F是AD上的点,且AE=EF=FD.连接BE、BF,使它们分别与AO相交于点G、H.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com