
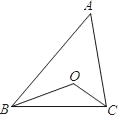
【题目】如图,△ABC中,下面说法正确的个数是( )个.
①若O是△ABC的外心,∠A=50°,则∠BOC=100°;
②若O是△ABC的内心,∠A=50°,则∠BOC=115°;
③若BC=6,AB+AC=10,则△ABC的面积的最大值是12;
④△ABC的面积是12,周长是16,则其内切圆的半径是1.
A. 1B. 2C. 3D. 4
【答案】C
【解析】
![]() 根据圆周角定理直接求出
根据圆周角定理直接求出![]() 的度数即可;
的度数即可;
![]() 利用内心的定义得出
利用内心的定义得出![]() 进而求出即可;
进而求出即可;
![]() 研究三角形面积最大值的问题,由于已知三边的和,故可以借助海伦公式建立面积关于边的函数,再利用基本不等式求最值;
研究三角形面积最大值的问题,由于已知三边的和,故可以借助海伦公式建立面积关于边的函数,再利用基本不等式求最值;
![]() 根据内心到三角形三边距离相等得出内切圆半径乘以周长等于面积,即可得出答案.
根据内心到三角形三边距离相等得出内切圆半径乘以周长等于面积,即可得出答案.
解:![]() 若O是
若O是![]() 的外心,
的外心,![]() ,则
,则![]() ,根据圆周角定理直接得出即可,故此选项正确;
,根据圆周角定理直接得出即可,故此选项正确;
![]() 若O是
若O是![]() 的内心,
的内心,![]() ,则
,则![]() ,故此选项正确;
,故此选项正确;
![]() 若
若![]() ,
,![]() ,则
,则![]() 的面积的最大值是12;
的面积的最大值是12;
由题意,三角形的周长是16,由令![]() ,则
,则![]() ,
,
由海伦公式可得三角形的面积
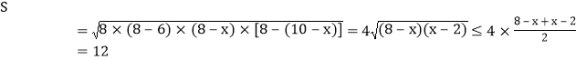 ,
,
等号仅当![]() 即
即![]() 时成立,
时成立,
故三角形的面积的最大值是12,故此选项正确;
![]() 的面积是12,周长是16,设内切圆半径为x,则
的面积是12,周长是16,设内切圆半径为x,则![]() ,
,
解得:![]() ,
,
则其内切圆的半径是1,此选项错误.
故正确的有![]() 共3个.
共3个.
故选:C.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
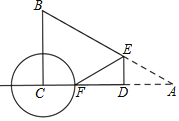
【题目】如图,在△ABC中,以AC为直径作⊙O交BC于点D,交AB于点G,且D是BC中点,DE⊥AB,垂足为E,交AC的延长线于点F.
(1)求证:直线EF是⊙O的切线;
(2)若CF=3,cosA=0.4,求出⊙O的半径和BE的长;
(3)连接CG,在(2)的条件下,求CG:EF的值.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC中,∠C=90°,∠A=30°,AB=4![]() .若动点D在线段AC上(不与点A、C重合),过点D作DE⊥AC交AB边于点E.点A关于点D的对称点为点F,以FC为半径作⊙C,当DE=_______时,⊙C与直线AB相切.
.若动点D在线段AC上(不与点A、C重合),过点D作DE⊥AC交AB边于点E.点A关于点D的对称点为点F,以FC为半径作⊙C,当DE=_______时,⊙C与直线AB相切.
查看答案和解析>>
科目:初中数学 来源: 题型:
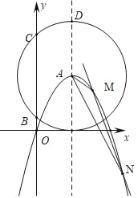
【题目】如图,抛物线L:y=﹣x2+bx+c经过坐标原点,与它的对称轴直线x=2交于A点.
(1)直接写出抛物线的解析式;
(2)⊙A与x轴相切,交y轴于B、C点,交抛物线L的对称轴于D点,恒过定点的直线y=kx﹣2k+8(k<0)与抛物线L交于M、N点,△AMN的面积等于2,试求:
①弧BC的长;
②k的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】2018年首届“进博会”期间,上海对周边道路进行限速行驶.道路![]() 段为监测区,
段为监测区,![]() 、
、![]() 为监测点(如图).已知,
为监测点(如图).已知,![]() 、
、![]() 、
、![]() 在同一条直线上,且
在同一条直线上,且![]() ,
,![]() 米,
米,![]() ,
,![]() .
.
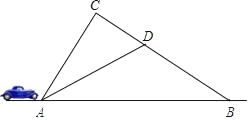
(1)求道路![]() 段的长;(精确到1米)
段的长;(精确到1米)
(2)如果![]() 段限速为60千米/时,一辆车通过
段限速为60千米/时,一辆车通过![]() 段的时间为90秒,请判断该车是否超速,并说明理由.(参考数据:
段的时间为90秒,请判断该车是否超速,并说明理由.(参考数据:![]()
![]() ,
,![]() ,
,![]() )
)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,⊙P的圆心P(m,n)在抛物线y=![]() 上.
上.
(1)写出m与n之间的关系式;
(2)当⊙P与两坐标轴都相切时,求出⊙P的半径;
(3)若⊙P的半径是8,且它在x轴上截得的弦MN,满足0≤MN≤2![]() 时,求出m、n的范围.
时,求出m、n的范围.

查看答案和解析>>
科目:初中数学 来源: 题型:
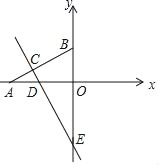
【题目】已知点A在x轴负半轴上,点B在y轴正半轴上,线段OB的长是方程x2﹣2x﹣8=0的解,tan∠BAO=![]() .
.
(1)求点A的坐标;
(2)点E在y轴负半轴上,直线EC⊥AB,交线段AB于点C,交x轴于点D,S△DOE=16.若反比例函数y=![]() 的图象经过点C,求k的值;
的图象经过点C,求k的值;
(3)在(2)条件下,点M是DO中点,点N,P,Q在直线BD或y轴上,是否存在点P,使四边形MNPQ是矩形?若存在,请直接写出点P的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,某消防队在一居民楼前进行演习,消防员利用云梯成功救出点B处的求救者后,又发现点B正上方点C处还有一名求救者.在消防车上点A处测得点B和点C的仰角分别是45°和65°,点A距地面2.5米,点B距地面10.5米.为救出点C处的求救者,云梯需要继续上升的高度BC约为多少米?(结果保留整数.参考数据:tan65°≈2.1,sin65°≈0.9,cos65°≈0.4,![]() ≈1.4)
≈1.4)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,二次函数y=ax2+bx+c的图象与x轴交于点A(﹣1,0),B(3,0).下列结论:①2a﹣b=0;②(a+c)2<b2;③当﹣1<x<3时,y<0;④当a=1时,将抛物线先向上平移2个单位,再向右平移1个单位,得到抛物线y=(x﹣2)2﹣2.其中正确的是( )
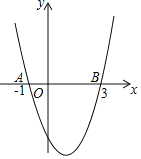
A. ①③ B. ②③ C. ②④ D. ③④
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com