
分析 (1)直接利用立方根的性质以及二次根式的性质化简求出答案;
(2)直接利用绝对值的性质化简,再利用二次根式乘法运算法则求出答案;
(3)首先利用二次根式以及立方根的性质化简各式进而求出答案.
解答 解:(1)$\root{3}{27}$+$\sqrt{(-3)^{2}}$
=3+3
=6;
(2)|-$\sqrt{3}$|×($\sqrt{3}$-$\frac{1}{\sqrt{3}}$)
=$\sqrt{3}$×($\sqrt{3}$-$\frac{1}{\sqrt{3}}$)
=3-1
=2;
(3)$\sqrt{0.09}$+$\root{3}{-8}$-$\sqrt{\frac{1}{4}}$
=0.3-2-$\frac{1}{2}$
=-2.2.
点评 此题主要考查了实数运算,正确利用相关性质化简各数是解题关键.


 科学实验活动册系列答案
科学实验活动册系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源:2017届浙江省平阳县名校九年级下学期第一次模拟统练数学试卷(解析版) 题型:判断题
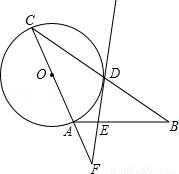
(本题10分)如图,在△ABC中,AB=AC,以AC为直径作⊙O交BC于点D,过点D作⊙O的切线,交AB于点E,交CA的延长线于点F.
(1)求证:FE⊥AB;
(2)当EF=6,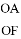 =
= 时,求DE的长.
时,求DE的长.
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | (2a-b)(2a+b) | B. | (x+2y)(-2y+x) | C. | (2a+b)(a-2b) | D. | (-x-y)(-x+y) |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 如图,点P1(x1,y1),点P2(x2,y2),…,点Pn(xn,yn)在函数$y=\frac{1}{x}$(x>0)的图象上,△P1OA1,△P2A1A2,△P3A2A3,…,△PnAn-1An都是等腰直角三角形,斜边OA1、A1A2、A2A3,…,An-1An都在x轴上(n是大于或等于2的正整数),若△P1OA2的内接正方形B1C1D1E2的周长记为l1,△P2A1A2的内接正方形B2C2D2E2的周长记为l2,…,△PnAn-1An的内接正方形BnCnDnEn的周长记为ln,则用含n的式子表示l1+l2+l3+…+ln为( )
如图,点P1(x1,y1),点P2(x2,y2),…,点Pn(xn,yn)在函数$y=\frac{1}{x}$(x>0)的图象上,△P1OA1,△P2A1A2,△P3A2A3,…,△PnAn-1An都是等腰直角三角形,斜边OA1、A1A2、A2A3,…,An-1An都在x轴上(n是大于或等于2的正整数),若△P1OA2的内接正方形B1C1D1E2的周长记为l1,△P2A1A2的内接正方形B2C2D2E2的周长记为l2,…,△PnAn-1An的内接正方形BnCnDnEn的周长记为ln,则用含n的式子表示l1+l2+l3+…+ln为( )| A. | $\frac{8\sqrt{n}}{3}$ | B. | 2$\sqrt{n}$ | C. | $\frac{4\sqrt{n}}{3}$ | D. | $\frac{2\sqrt{n}}{3}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com