
ЁОЬтФПЁПШчЭМЃЌжБЯпyЃНЉx+4гыxжсНЛгкЕуAЃЌгыyжсНЛгкЕуBЃЎХзЮяЯпyЃНЉ![]() x2+bx+cОЙ§AЃЌBСНЕуЃЌгыxжсЕФСэЭтвЛИіНЛЕуЮЊC
x2+bx+cОЙ§AЃЌBСНЕуЃЌгыxжсЕФСэЭтвЛИіНЛЕуЮЊC
ЃЈ1ЃЉЬюПеЃКbЃНЁЁ ЃЌcЃНЁЁ ЃЌЕуCЕФзјБъЮЊЁЁ ЃЎ
ЃЈ2ЃЉШчЭМ1ЃЌШєЕуPЪЧЕквЛЯѓЯоХзЮяЯпЩЯЕФЕуЃЌСЌНгOPНЛжБЯпABгкЕуQЃЌЩшЕуPЕФКсзјБъЮЊmЃЎPQгыOQЕФБШжЕЮЊyЃЌЧѓyгыmЕФЪ§бЇЙиЯЕЪНЃЌВЂЧѓГіPQгыOQЕФБШжЕЕФзюДѓжЕЃЎ
ЃЈ3ЃЉШчЭМ2ЃЌШєЕуPЪЧЕкЫФЯѓЯоЕФХзЮяЯпЩЯЕФвЛЕуЃЎСЌНгPBгыAPЃЌЕБЁЯPBA+ЁЯCBOЃН45ЁуЪБЃЎЧѓЁїPBAЕФУцЛ§ЃЎ

ЁОД№АИЁПЃЈ1ЃЉ1ЃЌ 4ЃЌCЃЈЉ2ЃЌ0ЃЉЃЛЃЈ2ЃЉyЃНЉ![]() m2+
m2+![]() m ЃЌPQгыOQЕФБШжЕЕФзюДѓжЕЮЊ
m ЃЌPQгыOQЕФБШжЕЕФзюДѓжЕЮЊ![]() ЃЛЃЈ3ЃЉSЁїPBAЃН12ЃЎ
ЃЛЃЈ3ЃЉSЁїPBAЃН12ЃЎ
ЁОНтЮіЁП
ЃЈ1ЃЉЭЈЙ§вЛДЮКЏЪ§НтЮіЪНШЗЖЈAЁЂBСНЕузјБъЃЌжБНгРћгУД§ЖЈЯЕЪ§ЗЈЧѓНтМДПЩЕУЕНbЃЌcЕФжЕЃЌСюy=0БуПЩЕУCЕузјБъЃЎ
ЃЈ2ЃЉЗжБ№Й§PЁЂQСНЕуЯђxжсзїДЙЯпЃЌЭЈЙ§PQгыOQЕФБШжЕЮЊyвдМАЦНааЯпЗжЯпЖЮГЩБШР§ЃЌевЕН![]() ЃЌЩшЕуPзјБъЮЊЃЈmЃЌ-
ЃЌЩшЕуPзјБъЮЊЃЈmЃЌ-![]() m2+m+4ЃЉЃЌQЕузјБъЃЈnЃЌ-n+4ЃЉЃЌБэЪОГіEDЁЂODЕШГЄЖШМДПЩЕУyгыmЁЂnжЎМфЕФЙиЯЕЃЌдйДЮРћгУ
m2+m+4ЃЉЃЌQЕузјБъЃЈnЃЌ-n+4ЃЉЃЌБэЪОГіEDЁЂODЕШГЄЖШМДПЩЕУyгыmЁЂnжЎМфЕФЙиЯЕЃЌдйДЮРћгУ![]() МДПЩЧѓНтЃЎ
МДПЩЧѓНтЃЎ
ЃЈ3ЃЉЧѓЕУPЕузјБъЃЌРћгУЭМаЮИюВЙЗЈЧѓНтМДПЩЃЎ
ЃЈ1ЃЉЁпжБЯпyЃНЉx+4гыxжсНЛгкЕуAЃЌгыyжсНЛгкЕуBЃЎ
ЁрAЃЈ4ЃЌ0ЃЉЃЌBЃЈ0ЃЌ4ЃЉЃЎ
гжЁпХзЮяЯпЙ§BЃЈ0ЃЌ4ЃЉ
ЁрcЃН4ЃЎ
АбAЃЈ4ЃЌ0ЃЉДњШыyЃНЉx2+bx+4ЕУЃЌ
0ЃНЉ![]() ЁС42+4b+4ЃЌНтЕУЃЌbЃН1ЃЎ
ЁС42+4b+4ЃЌНтЕУЃЌbЃН1ЃЎ
ЁрХзЮяЯпНтЮіЪНЮЊЃЌyЃНЉ![]() x2+x+4ЃЎ
x2+x+4ЃЎ
СюЉ![]() x2+x+4ЃН0ЃЌ
x2+x+4ЃН0ЃЌ
НтЕУЃЌxЃНЉ2ЛђxЃН4ЃЎ
ЁрCЃЈЉ2ЃЌ0ЃЉЃЎ
ЃЈ2ЃЉШчЭМ1ЃЌ
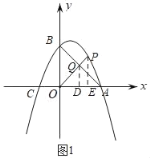
ЗжБ№Й§PЁЂQзїPEЁЂQDДЙжБгкxжсНЛxжсгкЕуEЁЂDЃЎ
ЩшPЃЈmЃЌЉ![]() m2+m+4ЃЉЃЌQЃЈnЃЌЉn+4ЃЉЃЌ
m2+m+4ЃЉЃЌQЃЈnЃЌЉn+4ЃЉЃЌ
дђPEЃНЉ![]() m2+m+4ЃЌQDЃНЉn+4ЃЎ
m2+m+4ЃЌQDЃНЉn+4ЃЎ
гжЁп![]() ЃНyЃЎ
ЃНyЃЎ
ЁрnЃН![]() ЃЎ
ЃЎ
гжЁп![]() ЃЌМД
ЃЌМД
АбnЃН![]() ДњШыЩЯЪНЕУЃЌ
ДњШыЩЯЪНЕУЃЌ

ећРэЕУЃЌ4yЃНЉ![]() m2+2mЃЎ
m2+2mЃЎ
ЁрyЃНЉ![]() m2+
m2+![]() mЃЎ
mЃЎ
ymaxЃН ЃЎ
ЃЎ
МДPQгыOQЕФБШжЕЕФзюДѓжЕЮЊ![]() ЃЎ
ЃЎ
ЃЈ3ЃЉШчЭМ2ЃЌ
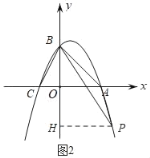
ЁпЁЯOBAЃНЁЯOBP+ЁЯPBAЃН45Ёу
ЁЯPBA+ЁЯCBOЃН45Ёу
ЁрЁЯOBPЃНЁЯCBO
ДЫЪБPBЙ§ЕуЃЈ2ЃЌ0ЃЉЃЎ
ЩшжБЯпPBНтЮіЪНЮЊЃЌyЃНkx+4ЃЎ
АбЕуЃЈ2ЃЌ0ЃЉДњШыЩЯЪНЕУЃЌ0ЃН2k+4ЃЎ
НтЕУЃЌkЃНЉ2
ЁржБЯпPBНтЮіЪНЮЊЃЌyЃНЉ2x+4ЃЎ
СюЉ2x+4ЃНЉ![]() x2+x+4
x2+x+4
ећРэЕУЃЌ![]() x2Љ3xЃН0ЃЎ
x2Љ3xЃН0ЃЎ
НтЕУЃЌxЃН0ЃЈЩсШЅЃЉЛђxЃН6ЃЎ
ЕБxЃН6ЪБЃЌЉ2x+4ЃНЉ2ЁС6+4ЃНЉ8
ЁрPЃЈ6ЃЌЉ8ЃЉЃЎ
Й§PзїPHЁЭcyжсгкЕуHЃЎ
дђSЫФБпаЮOHPAЃН![]() ЃЈOA+PHЃЉOHЃН
ЃЈOA+PHЃЉOHЃН![]() ЃЈ4+6ЃЉЁС8ЃН40ЃЎ
ЃЈ4+6ЃЉЁС8ЃН40ЃЎ
SЁїOABЃН![]() OAOBЃН
OAOBЃН![]() ЁС4ЁС4ЃН8ЃЎ
ЁС4ЁС4ЃН8ЃЎ
SЁїBHPЃН![]() PHBHЃН
PHBHЃН![]() ЁС6ЁС12ЃН36ЃЎ
ЁС6ЁС12ЃН36ЃЎ
ЁрSЁїPBAЃНSЫФБпаЮOHPA+SЁїOABЉSЁїBHPЃН40+8Љ36ЃН12ЃЎ



| ФъМЖ | ИпжаПЮГЬ | ФъМЖ | ГѕжаПЮГЬ |
| ИпвЛ | ИпвЛУтЗбПЮГЬЭЦМіЃЁ | ГѕвЛ | ГѕвЛУтЗбПЮГЬЭЦМіЃЁ |
| ИпЖў | ИпЖўУтЗбПЮГЬЭЦМіЃЁ | ГѕЖў | ГѕЖўУтЗбПЮГЬЭЦМіЃЁ |
| ИпШ§ | ИпШ§УтЗбПЮГЬЭЦМіЃЁ | ГѕШ§ | ГѕШ§УтЗбПЮГЬЭЦМіЃЁ |
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПдкЭЌвЛЦНУцжБНЧзјБъЯЕжаЃЌКЏЪ§![]() гы
гы![]() ЕФЭМЯѓПЩФмЪЧЃЈ ЃЉ
ЕФЭМЯѓПЩФмЪЧЃЈ ЃЉ
A. B.
B. C.
C. D.
D.
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПАбвЛИБШ§НЧАхАДШчЭМ1ЫљЪОЗХжУЃЌЦфжаЕу![]() дк
дк![]() БпЩЯЃЌ
БпЩЯЃЌ![]() ЃЌаББп
ЃЌаББп![]() .НЋШ§НЧАх
.НЋШ§НЧАх![]() ШЦЕу
ШЦЕу![]() ЫГЪБеыа§зЊЃЌМЧа§зЊНЧЮЊ
ЫГЪБеыа§зЊЃЌМЧа§зЊНЧЮЊ![]() .
.
ЃЈ1ЃЉдкЭМ1жаЃЌЩш![]() гы
гы![]() ЕФНЛЕуЮЊ
ЕФНЛЕуЮЊ![]() ЃЌдђЯпЖЮAFЕФГЄЮЊ ЃЛ
ЃЌдђЯпЖЮAFЕФГЄЮЊ ЃЛ

ЃЈ2ЃЉЕБ![]() ЪБЃЌШ§НЧАх
ЪБЃЌШ§НЧАх![]() а§зЊЕН
а§зЊЕН![]() ЃЌЕФЮЛжУ(ШчЭМ2ЫљЪО)ЃЌСЌНг
ЃЌЕФЮЛжУ(ШчЭМ2ЫљЪО)ЃЌСЌНг![]() ЃЌЧыХаЖЯЫФБпаЮ
ЃЌЧыХаЖЯЫФБпаЮ![]() ЕФаЮзДЃЌВЂжЄУїФуЕФНсТл;
ЕФаЮзДЃЌВЂжЄУїФуЕФНсТл;

(3)ЕБШ§НЧАх![]() а§зЊЕН
а§зЊЕН![]() ЕФЮЛжУ(ШчЭМ3ЫљЪО)ЪБЃЌДЫЪБЕу
ЕФЮЛжУ(ШчЭМ3ЫљЪО)ЪБЃЌДЫЪБЕу![]() ЧЁКУдк
ЧЁКУдк![]() ЕФбгГЄЯпЩЯ.ЂйЧѓа§зЊНЧ
ЕФбгГЄЯпЩЯ.ЂйЧѓа§зЊНЧ![]() ЕФЖШЪ§;ЂкЧѓЯпЖЮ
ЕФЖШЪ§;ЂкЧѓЯпЖЮ![]() ЕФГЄ.
ЕФГЄ.

ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПФГЩЬГЁЙКНјвЛжжУПМўМлИёЮЊ100дЊЕФаТЩЬЦЗЃЌдкЩЬГЁЪдЯњЗЂЯжЃКЯњЪлЕЅМлx(дЊ/Мў)гыУПЬьЯњЪлСПy(Мў)жЎМфТњзуШчЭМЫљЪОЕФЙиЯЕЃК
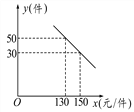
(1)ЧѓГіyгыxжЎМфЕФКЏЪ§ЙиЯЕЪНЃЛ
(2)аДГіУПЬьЕФРћШѓWгыЯњЪлЕЅМлxжЎМфЕФКЏЪ§ЙиЯЕЪНЃЛШєФуЪЧЩЬГЁИКд№ШЫЃЌЛсНЋЪлМлЖЈЮЊЖрЩйЃЌРДБЃжЄУПЬьЛёЕУЕФРћШѓзюДѓЃЌзюДѓРћШѓЪЧЖрЩйЃП
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПЦРМлзщЖдФГЧјОХФъМЖНЬЪІЕФЪдОэНВЦРПЮЕФбЇЩњВЮгыЖШНјааЦРМлЕїВщЃЌЦфЦРМлЯюФПЮЊжїЖЏжЪвЩЁЂЖРСЂЫМПМЁЂзЈзЂЬ§НВЁЂНВНтЬтФПЫФЯюЃЎЦРМлзщЫцЛњГщШЁСЫШєИЩУћЭЌбЇЕФВЮгыЧщПіЃЌЛцжЦГЩШчЭМЫљЪОЕФЩШаЮЭГМЦЭМКЭЬѕаЮЭГМЦЭМЃЈОљВЛЭъећЃЉЃЌЧыИљОнЭМжаЫљИјаХЯЂНтД№ЯТСаЮЪЬтЃК
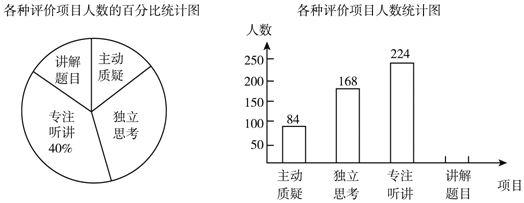
(1)дкетДЮЦРМлжаЃЌвЛЙВГщВщСЫЁЁ ЁЁУћЭЌбЇЃЛ
(2)ЧыНЋЬѕаЮЭГМЦЭМВЙГфЭъећЃЛ
(3)ШчЙћШЋЧјга6000УћОХФъМЖбЇЩњЃЌФЧУДдкЪдОэЦРНВПЮжаЃЌЁАЖРСЂЫМПМЁБЕФдМгаЖрЩйШЫЃП
(4)ИљОнЭГМЦЗДгГЕФЧщПіЃЌЧыФуЖдИУЧјЕФОХФъМЖЭЌбЇЬсГівЛЬѕЖдД§ЪдОэНВЦРПЮЕФНЈвщЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПжВЪїНкЦкМфЃЌФГЕЅЮЛгћЙКНјAЁЂBСНжжЪїУчЃЌШєЙКНјAжжЪїУч3ПУЃЌBжжЪїУч5ПУЃЌаш2100дЊЃЌШєЙКНјAжжЪїУч4ПУЃЌBжжЪїУч10ПУЃЌаш3800дЊЃЎ
ЃЈ1ЃЉЧѓЙКНјAЁЂBСНжжЪїУчЕФЕЅМлЃЛ
ЃЈ2ЃЉШєИУЕЅЮЛзМБИгУВЛЖргк8000дЊЕФЧЎЙКНјетСНжжЪїУчЙВ30ПУЃЌЧѓAжжЪїУчжСЩйашЙКНјЖрЩйПУЃП
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
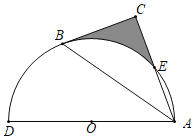
ЁОЬтФПЁПШчЭМЃЌвдADЮЊжБОЖЕФАыдВOОЙ§RtЁїABCаББпABЕФСНИіЖЫЕуЃЌНЛжБНЧБпACгкЕуEЃЛBЁЂEЪЧАыдВЛЁЕФШ§ЕШЗжЕуЃЌ![]() ЕФГЄЮЊ
ЕФГЄЮЊ![]() ЃЌдђЭМжавѕгАВПЗжЕФУцЛ§ЮЊЃЈЁЁЁЁЃЉ
ЃЌдђЭМжавѕгАВПЗжЕФУцЛ§ЮЊЃЈЁЁЁЁЃЉ
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
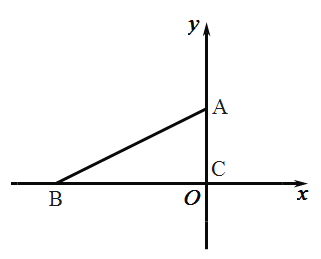
ЁОЬтФПЁПШчЭМЃЌвбжЊжБЯп![]() гыxжсЁЂyжсЗжБ№НЛгкAЁЂBСНЕуЃЌPЪЧвдCЃЈ0ЃЌ1ЃЉЮЊдВаФЃЌ1ЮЊАыОЖЕФдВЩЯвЛЖЏЕуЃЌСЌНсPAЁЂPBЃЎдђЁїPABУцЛ§ЕФзюДѓжЕЪЧЃЈ ЃЉ
гыxжсЁЂyжсЗжБ№НЛгкAЁЂBСНЕуЃЌPЪЧвдCЃЈ0ЃЌ1ЃЉЮЊдВаФЃЌ1ЮЊАыОЖЕФдВЩЯвЛЖЏЕуЃЌСЌНсPAЁЂPBЃЎдђЁїPABУцЛ§ЕФзюДѓжЕЪЧЃЈ ЃЉ

A.8B.12C.![]() D.
D.![]()
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПдк![]() жНЦЌжаЃЌ
жНЦЌжаЃЌ![]() ЃЌ
ЃЌ![]() ЃЌ
ЃЌ![]() .ШчЭМЃЌжБНЧЖЅЕу
.ШчЭМЃЌжБНЧЖЅЕу![]() дкдЕуЃЌЕу
дкдЕуЃЌЕу![]() дк
дк![]() жсИКАыжсЩЯЃЌЕБЕу
жсИКАыжсЩЯЃЌЕБЕу![]() дк
дк![]() жсЩЯЯђЩЯвЦЖЏЪБЃЌЕу
жсЩЯЯђЩЯвЦЖЏЪБЃЌЕу![]() вВЫцжЎдк
вВЫцжЎдк![]() жсЩЯЯђгввЦЖЏЃЌЕБЕу
жсЩЯЯђгввЦЖЏЃЌЕБЕу![]() ЕНДядЕуЪБЃЌЕу
ЕНДядЕуЪБЃЌЕу![]() ЭЃжЙвЦЖЏ.дквЦЖЏЙ§ГЬжаЃЌЕу
ЭЃжЙвЦЖЏ.дквЦЖЏЙ§ГЬжаЃЌЕу![]() ЕНдЕуЕФзюДѓОрРыЪЧ__________ЃЎ
ЕНдЕуЕФзюДѓОрРыЪЧ__________ЃЎ
ВщПДД№АИКЭНтЮі>>
АйЖШжТаХ - СЗЯАВсСаБэ - ЪдЬтСаБэ
КўББЪЁЛЅСЊЭјЮЅЗЈКЭВЛСМаХЯЂОйБЈЦНЬЈ | ЭјЩЯгаКІаХЯЂОйБЈзЈЧј | ЕчаХеЉЦОйБЈзЈЧј | ЩцРњЪЗащЮожївхгаКІаХЯЂОйБЈзЈЧј | ЩцЦѓЧжШЈОйБЈзЈЧј
ЮЅЗЈКЭВЛСМаХЯЂОйБЈЕчЛАЃК027-86699610 ОйБЈгЪЯфЃК58377363@163.com