
【题目】如图,⊙M的半径为4,圆心M的坐标为(6,8),点P是⊙M上的任意一点,PA⊥PB,且PA、PB与x轴分别交于A、B两点,若点A、点B关于原点O对称,则AB的最小值为____.

科目:初中数学 来源: 题型:
【题目】如图,二次函数y=ax2+bx+c(a≠0)的图象经过点A,B,C.现有下面四个推断:①抛物线开口向下;②当x=-2时,y取最大值;③当m<4时,关于x的一元二次方程ax2+bx+c=m必有两个不相等的实数根;④直线y=kx+c(k≠0)经过点A,C,当kx+c> ax2+bx+c时,x的取值范围是-4<x<0;其中推断正确的是 ( )
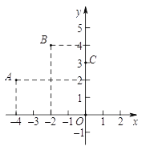
A. ①②B. ①③C. ①③④D. ②③④
查看答案和解析>>
科目:初中数学 来源: 题型:
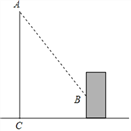
【题目】小左同学想利用影长测量学校旗杆的高度,如图,她在某一时刻立一长度为1米的标杆,测得其影长为![]() 米,同时旗杆投影的一部分在地上,另一部分在某一建筑物的墙上,测得旗杆与建筑物的距离为10米,旗杆在墙上的影高为2米,请帮小左同学算出学校旗杆的高度.
米,同时旗杆投影的一部分在地上,另一部分在某一建筑物的墙上,测得旗杆与建筑物的距离为10米,旗杆在墙上的影高为2米,请帮小左同学算出学校旗杆的高度.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】今年下半年以来,猪肉价格不断上涨,主要是由非洲猪瘟疫情导致.非洲猪瘟疫情发病急,蔓延速度快.某养猪场第一天发现3头生猪发病,两天后发现共有192头生猪发病.
(1)求每头发病生猪平均每天传染多少头生猪?
(2)若疫情得不到有效控制,按照这样的传染速度,3天后生猪发病头数会超过1500头吗?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)【问题发现】
如图1,在Rt△ABC中,AB=AC=2,∠BAC=90°,点D为BC的中点,以CD为一边作正方形CDEF,点E恰好与点A重合,则线段BE与AF的数量关系为
(2)【拓展研究】
在(1)的条件下,如果正方形CDEF绕点C旋转,连接BE,CE,AF,线段BE与AF的数量关系有无变化?请仅就图2的情形给出证明;
(3)【问题发现】
当正方形CDEF旋转到B,E,F三点共线时候,直接写出线段AF的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
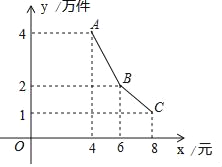
【题目】为了支持大学生创业,某市政府出台了一项优惠政策:提供10万元的无息创业贷款.小王利用这笔贷款,注册了一家淘宝网店,招收5名员工,销售一种火爆的电子产品,并约定用该网店经营的利润,逐月偿还这笔无息贷款.已知该产品的成本为每件4元,员工每人每月的工资为4千元,该网店还需每月支付其它费用1万元.该产品每月销售量y(万件)与销售单价x(元)万件之间的函数关系如图所示.
(1)求该网店每月利润w(万元)与销售单价x(元)之间的函数表达式;
(2)小王自网店开业起,最快在第几个月可还清10万元的无息贷款?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】综合与探究:
如图所示,在平面直角坐标系中,直线![]() 与反比例函数
与反比例函数![]() 的图象交于
的图象交于![]() ,
,![]() 两点,过点
两点,过点![]() 作
作![]() 轴于点
轴于点![]() ,过点
,过点![]() 作
作![]() 轴于点
轴于点![]() .
.
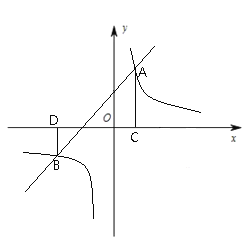
(1)求![]() ,
,![]() 的值及反比例函数的函数表达式;
的值及反比例函数的函数表达式;
(2)若点![]() 在线段
在线段![]() 上,且
上,且![]() ,请求出此时点
,请求出此时点![]() 的坐标;
的坐标;
(3)小颖在探索中发现:在![]() 轴正半轴上存在点
轴正半轴上存在点![]() ,使得
,使得![]() 是以
是以![]() 为顶角的等腰三角形.请你直接写出点
为顶角的等腰三角形.请你直接写出点![]() 的坐标.
的坐标.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com