
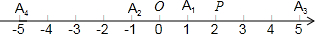
 口算题卡加应用题集训系列答案
口算题卡加应用题集训系列答案 综合自测系列答案
综合自测系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
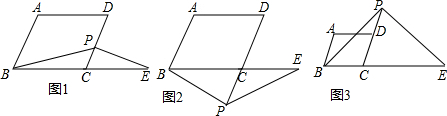
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
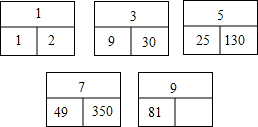
科目:初中数学 来源: 题型:解答题
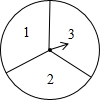 2015年1月9日,2014年度国家科学技术奖励大会在北京人民大会堂举行.为了加强青少年科技创新的意识,某市举办了科学表演大赛.小丽和小红想利用转转盘的游戏决定谁去参加该大赛,游戏规则如下:如图是一个可以自由转动的转盘,被平均分成3个扇形,扇形上分别标有数字1,2,3,转动一次转盘,任其自由停止,指针会指向某个扇形(若指针指在分界线上,则重转),相应地得到一个数字,两人各转动一次,若得到的两个数字之和为偶数,则小丽去参赛,否则小红去参赛.
2015年1月9日,2014年度国家科学技术奖励大会在北京人民大会堂举行.为了加强青少年科技创新的意识,某市举办了科学表演大赛.小丽和小红想利用转转盘的游戏决定谁去参加该大赛,游戏规则如下:如图是一个可以自由转动的转盘,被平均分成3个扇形,扇形上分别标有数字1,2,3,转动一次转盘,任其自由停止,指针会指向某个扇形(若指针指在分界线上,则重转),相应地得到一个数字,两人各转动一次,若得到的两个数字之和为偶数,则小丽去参赛,否则小红去参赛.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com