
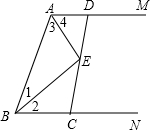
 如图,过线段AB的两个端点作射线AM、BN,使AM∥BN,∠MAB、∠NBA的平分线交于E.
如图,过线段AB的两个端点作射线AM、BN,使AM∥BN,∠MAB、∠NBA的平分线交于E.| 1 |
| 2 |
| 1 |
| 2 |
 延长AE交BN于F,
延长AE交BN于F,| DE |
| CE |
| AE |
| EF |
| AD |
| CF |
| AE |
| EF |


 状元坊全程突破导练测系列答案
状元坊全程突破导练测系列答案科目:初中数学 来源: 题型:
 在北京召开的国际数学家大会会标如图所示,它是由四个相同的直角三角形与中间的小正方形拼成的一个大正方形,若大正方形的面积是13,小正方形的面积是1,直角三角形的较长直角边为a,较短直角边为b,则a4+b4的值为( )
在北京召开的国际数学家大会会标如图所示,它是由四个相同的直角三角形与中间的小正方形拼成的一个大正方形,若大正方形的面积是13,小正方形的面积是1,直角三角形的较长直角边为a,较短直角边为b,则a4+b4的值为( )| A、35 | B、43 | C、89 | D、97 |
查看答案和解析>>
科目:初中数学 来源: 题型:
 如图,直线y=-x+2
如图,直线y=-x+2| 3 |
| k |
| x |
查看答案和解析>>
科目:初中数学 来源: 题型:
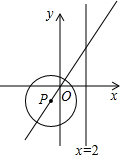 如图,P为正比例函数y=
如图,P为正比例函数y=| 3 |
| 2 |
查看答案和解析>>
科目:初中数学 来源: 题型:
A、如果s=vt,那么v=
| ||
B、如果
| ||
| C、如果x-3=y-3,那么x=y | ||
| D、如果a=b,那么a+b=b-a |
查看答案和解析>>
科目:初中数学 来源: 题型:
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com