
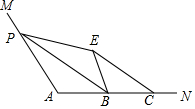
 如图,∠A=110°,在边AN上取B,C,使AB=BC.点P为边AM上一点,将△APB沿PB折叠,使点A落在角内点E处,连接CE,则∠BPE+∠BCE=70°.
如图,∠A=110°,在边AN上取B,C,使AB=BC.点P为边AM上一点,将△APB沿PB折叠,使点A落在角内点E处,连接CE,则∠BPE+∠BCE=70°. 分析 根据折叠的性质得到∠APB=∠BPE,AB=BE,∠BEP=∠A=110°,根据等腰三角形的性质得到∠BEC=∠BCE,根据四边形的内角和即可得到结论.
解答  解:∵△APB沿PB折叠,得到△PEB,
解:∵△APB沿PB折叠,得到△PEB,
∴∠APB=∠BPE,AB=BE,∠BEP=∠A=110°,
∵AB=BC,
∴BC=BE,
∴∠BEC=∠BCE,
∴∠BPE+∠BCE=∠APB+∠BEC,
∵∠BPE+∠BCE+∠APB+∠BEC=360°-∠A-∠BEP=140°,
∴∠BPE+∠BCE=70°,
故答案为:70.
点评 本题考查了翻折变换(折叠问题),等腰三角形的性质,四边形的内角和,熟练掌握折叠的性质是解题的关键.


 期末冲刺100分创新金卷完全试卷系列答案
期末冲刺100分创新金卷完全试卷系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
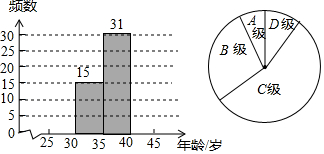 菲尔兹奖是国际上享有崇高声誉的一个数学奖项,每4年评选一次,颁给有卓越贡献的年轻数学家,被视为数学界的诺贝尔奖.下面的数据是从1936年至2014年45岁以下菲尔兹奖得住获奖时的年龄(岁):
菲尔兹奖是国际上享有崇高声誉的一个数学奖项,每4年评选一次,颁给有卓越贡献的年轻数学家,被视为数学界的诺贝尔奖.下面的数据是从1936年至2014年45岁以下菲尔兹奖得住获奖时的年龄(岁):| 分组 | 频数 |
| A:25~30 | 1 |
| B:30~35 | 15 |
| C:35~40 | 31 |
| D:40~45 | 3 |
| 总 计 | 50 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
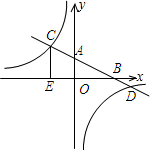 如图,在平面直角坐标系xOy中,一次函数y1=ax+b的图象分别与x,y轴交于点B,A,与反比例函数y2=$\frac{m}{x}$的图象交于点C,D,CE⊥x轴于点E,tan∠ABO=$\frac{1}{2}$,OB=4,OE=2.
如图,在平面直角坐标系xOy中,一次函数y1=ax+b的图象分别与x,y轴交于点B,A,与反比例函数y2=$\frac{m}{x}$的图象交于点C,D,CE⊥x轴于点E,tan∠ABO=$\frac{1}{2}$,OB=4,OE=2.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com