练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    【题目】如图，在△ABC中，AD平分∠BAC,按如下步骤作图：第一步，分别以点A、D为圆心，以大于的长为半径在AD的两侧作弧，交于两点M、N;第二步，连结MN，分别交AB、AC于点E、F；第三步，连结DE、DF．．若BD=6，AF=4，CD=3，则BE的长是（ ）

    A. 2 B. 4 C. 6 D. 8

    【答案】D

    【解析】试题分析：∵根据作法可知：MN是线段AD的垂直平分线，∴AE=DE，AF=DF，∴∠EAD=∠EDA，∵AD平分∠BAC，∴∠BAD=∠CAD，∴∠EDA=∠CAD，∴DE∥AC，同理DF∥AE，∴四边形AEDF是菱形，∴AE=DE=DF=AF，∵AF=4，∴AE=DE=DF=AF=4，∵DE∥AC，∴=，∵BD=6，AE=4，CD=3，∴=，∴BE=8，故选D．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    【题目】AB是⊙O的直径，AC、AD是⊙O的两弦，已知AB=16，AC=8，AD=，求∠DAC的度数．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

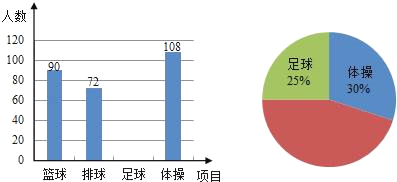
    【题目】某中学进行体育教学改革，同时开设篮球、排球、足球、体操课、学生可根据自己的爱好任选其一，体育老师根据七年级学生的报名情况进行了统计，并绘制了下面尚未完整的条形统计图和扇形统计图．请根据统计图解答下列问题：

    （1）该校七年级共有多少名学生？

    （2）将两个统计图补充完整；

    （3）从统计图中你还能得到哪些信息？（写出两条即可）

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】在同样条件下对某种小麦种子进行发芽试验，统计发芽种子数，获得如下频数表．

    试验种子n（粒）

    1

    5

    50

    100

    200

    500

    1000

    2000

    3000

    发芽频数m

    1

    4

    45

    92

    188

    476

    951

    1900

    2850

    发芽频率

    0

    0.80

    0.90

    0.92

    0.94

    0.952

    0.951

    a

    b

    （1）计算表中a，b的值；

    （2）估计该麦种的发芽概率；

    （3）如果该麦种发芽后，只有87%的麦芽可以成活，现有100kg麦种，则有多少千克的麦种可以成活为秧苗？

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】在一个不透明的盒子里装有只有颜色不同的黑、白两种球共40个，小丽做摸球实验，她将盒子里面的球搅匀后从中随机摸出一个球记下颜色，再把它放回盒子中，不断重复上述过程，下表是实验中的一组统计数据：

    摸球的次数n

    100

    200

    300

    500

    800

    1000

    3000

    摸到白球的次数m

    63

    124

    178

    302

    481

    599

    1803

    摸到白球的频率

    0.63

    0.62

    0.593

    0.604

    0.601

    0.599

    0.601

    （1）请估计：当实验次数为10000次时，摸到白球的频率将会接近　 　；（精确到0.1）

    （2）假如由你摸球一次，你摸到白球的概率P（摸到白球）=　 　；

    （3）盒子中有黑球　 　个．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

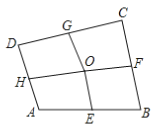
    【题目】如图，四边形ABCD中，E、F、G、H依次是各边中点，O是形内一点，若四边形AEOH、四边形BFOE、四边形CGOF的面积分别是4、5、8,则四边形DHOG的面积是________.

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】按要求解一元二次方程

    （1）4x2﹣8x+1=0（配方法） （2）7x（5x+2）=6（5x+2）（因式分解法）

    （3）3x2+5（2x+1）=0（公式法） （4）x2﹣2x﹣8=0．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】在《九章算术》中有求三角形面积公式“底乘高的一半”，但是在实际丈量土地面积时，量出高并非易事，所以古人想到了能否利用三角形的三条边长来求面积．我国南宋著名的数学家秦九韶（年—年）提出了“三斜求积术”，阐述了利用三角形三边长求三角形面积方法，简称秦九韶公式．在海伦（公元年左右，生平不详）的著作《测地术》中也记录了利用三角形三边长求三角形面积的方法，相传这个公式最早是由古希腊数学家阿基米德（公元前年—公元前年）得出的，故我国称这个公式为海伦一秦九韶公式．它的表达为：三角形三边长分别为、、，则三角形的面积（公式里的为半周长即周长的一半）．

    请利用海伦一秦九韶公式解决以下问题：

    （）三边长分别为、、的三角形面积为__________．

    （）四边形中，，，，，，四边形的面积为__________．

    （）五边形中，，，，，，，五边形的面积为__________．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】在平面直角坐标系xOy中，直线AB交y轴于A点，交x轴于B点， .

    已知点，写出点D关于直线AB对称的点的坐标；

    现在一直角三角板的直角顶点放置于AB的中点C，并绕C点旋转，两直角边分别交x轴、y轴于N、如图两点，求证： ；

    若E是线段OB上一点， 于G，交AB于F，求的值．

    查看答案和解析>>

    同步练习册答案