
����Ŀ��(1)��ͼ(1),��֪���ڡ�ABC��,��BAC=90��,AB=AC,ֱ��m������A,BD��ֱ��m,CE��ֱ��m,����ֱ�Ϊ��D,֤��:��ABD�ա�ACE��DE=BD+CE��
(2)��ͼ(2),��(1)�е�������Ϊ���ڡ�ABC�У�AB=AC��D, A, E���㶼��ֱ��m�ϣ������С�BDA=��AEC=��BAC=a������aΪ������ǻ�۽ǣ����ʽ���DE=BD+CE�Ƿ����?��������������֤����������������˵������.

���𰸡�(1)��������(2)���������ɼ�������
��������
��1������BD��ֱ��m��CE��ֱ��m�á�BDA=��CEA=90��������BAC=90�������ݵȽǵ������ȵá�CAE=��ABD��Ȼ�������AAS�����ж���ADB�ա�CEA��
��AE=BD��AD=CE������DE=AE+AD=BD+CE��
��2�����á�BDA=��BAC=�������DBA+��BAD=��BAD+��CAE=180��-�����ó���CAE=��ABD�������ó���ADB�ա�CEA���ɵó��𰸣�
(1)��BD��ֱ��m��CE��ֱ��m��
���BDA=��CEA=90����
�ߡ�BAC=90��
���BAD+��CAE=90����
�ߡ�BAD+��ABD=90����
���CAE=��ABD��
���ڡ�ADB�͡�CEA��
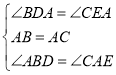
���ADB�ա�CEA(AAS)��
��AE=BD��AD=CE��
��DE=AE+AD=BD+CE��
(2)�ߡ�BDA=��BAC=����
���DBA+��BAD=��BAD+��CAE=180�����
���CAE=��ABD��
���ڡ�ADB�͡�CEA��
 ��
��
���ADB�ա�CEA(AAS)��
��AE=BD��AD=CE��
��DE=AE+AD=BD+CE.


 Сѧ��10���ӿ������100��ϵ�д�
Сѧ��10���ӿ������100��ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����2013���Ĵ���֦��12�֣���ͼ��������y=ax2+bx+c������A����3��0����B��1.0����C��0����3����

��1���������ߵĽ���ʽ��
��2������PΪ�����������������ϵ�һ�㣬����PAC�����ΪS����S�����ֵ�������ʱ��P�����ꣻ
��3���������ߵĶ���ΪD��DE��x���ڵ�E����y�����Ƿ���ڵ�M��ʹ����ADM��ֱ�������Σ������ڣ���ֱ��д����M�����ꣻ�������ڣ���˵�����ɣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������ij��ѧ�������й���У�����������ִ������ߡ����в����ݳ����ɼ�����ѡ��5��ѡ����ɳ��д����Ӻ��д����Ӳμ�ѧУ�����������Ӹ�ѡ����5��ѡ�ֵľ����ɼ���ͼ��ʾ��

��1������ͼʾ��д�±���
ƽ�������֣� | ��λ�����֣� | �������֣� | |
���в� | 85 | ||
���в� | 85 | 100 |
��2��������ӳɼ���ƽ��������λ���������ĸ��ӵľ����ɼ��Ϻã�
��3���������Ӿ����ɼ��ķ���ж���һ��������ѡ�ֳɼ���Ϊ�ȶ���
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���߹���ͼ������A����ֱ��l�ĶԳƵ�A'.
��֪��ֱ��l��l��һ��A.
��������A����l�ĶԳƵ�A'.
����������l����ȡһ��P���Ե�PΪԲ�ģ�PA��Ϊ�뾶���£���l�ڵ�B�����Ե�BΪԲ�ģ�AB��Ϊ�뾶����������AB�ڵ�A'. ��A'�����������ĶԳƵ�.
�ɲ���٣���________
�ɲ���ڣ���________
�������ϵ�������д��������˵����A��A'����ֱ��l�ԳƵ�����________.


�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ�����������ϵ�У�����0ABC�Ķ���A��C���������ϣ���B��4��2��������D��0��3����E��6��0����ֱ�߷ֱ���AB��BC���ڵ�M��N��
��1����ֱ��DE�ĺ�������ʽ�͵�M��N�����ꣻ
��2��������y��![]() ��k��0��kΪ������������M����ú����ı���ʽ�����ж���N�Ƿ��ڸú�����ͼ���ϣ�
��k��0��kΪ������������M����ú����ı���ʽ�����ж���N�Ƿ��ڸú�����ͼ���ϣ�
��3�����OMN�����S��
��4��������y��![]() ��k��0��kΪ��������ͼ�����BMNû�н��㣬���ֱ��д��k��ȡֵ��Ȧ����������̣�
��k��0��kΪ��������ͼ�����BMNû�н��㣬���ֱ��д��k��ȡֵ��Ȧ����������̣�

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��������y=ax2+bx��a��0����A��4��0����B��1��3�����㣬��C��B���������ߵĶԳ���Գƣ�����B��ֱ��BH��x�ᣬ��x���ڵ�H��
��1���������ߵı���ʽ��
��2�����C�����꣬�������ABC�������
��3����P����������һ���㣬��λ�ڵ������ޣ��Ƿ���������ĵ�P��ʹ����ABP�����Ϊ��ABC�����2���������ڣ������P�����꣬�������ڣ���˵�����ɣ�

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪һ�κ���y=��2m+3��x+m-1��
��1��������ͼ��ԭ�㣬��m��ֵ��
��2��������ͼ����y���ϵĽؾ�Ϊ-3����m��ֵ��
��3�����ú�����ֵy���Ա���x���������С����m��ȡֵ��Χ��
��4���ú���ͼ�����ڶ����ޣ���m��ȡֵ��Χ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij��ij��װ������ҵ�н���һ���Ϻ����������Ʒ������ҵ��Ϊ��ȷ������������ҵ���������������ǹ��ù����![]() �ı������Ϊԭ���ϣ�ÿ�ű�����ٰ��ղ÷�һ��÷�������
�ı������Ϊԭ���ϣ�ÿ�ű�����ٰ��ղ÷�һ��÷�������![]() ����
����![]() �����ְ�ģ���ͼ����ʾ������λ
�����ְ�ģ���ͼ����ʾ������λ![]() ��
��
��1���г����̣��飩�����ͼ����![]() ��
��![]() ��ֵ��
��ֵ��
��2�����������Σ�����625�ű�����ò÷�һ�ü���125�ű�����ò÷����ü����ٽ��õ���![]() ����
����![]() �Ͱ��������͵��棬�պÿ�������ͼ�ҵ���ʽ���ʽ��������Ʒ�У����������ʽ���ʽ��������Ʒ�и����ٸ���
�Ͱ��������͵��棬�պÿ�������ͼ�ҵ���ʽ���ʽ��������Ʒ�У����������ʽ���ʽ��������Ʒ�и����ٸ���


�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
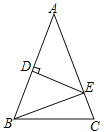
����Ŀ����3�֣���ͼ����ABC�У�AB=AC��AB�Ĵ�ֱƽ���߽���AB��D�㣬����AC��E�㣬����ABC����EBC���ܳ��ֱ���40cm��24cm����AB= cm��
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com