练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

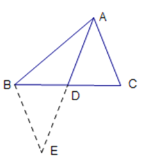
    【题目】仔细阅读下面的解题过程，并完成填空：如图13，AD为△ABC的中线，已知AD=4cm,试确定AB+AC的取值范围.

    解：延长AD到E,使DE = AD,连接BE.

    因为AD为△ABC的中线，

    所以BD=CD.

    在△ACD和△EBD中，因为AD=DE,∠ADC=∠EDB,CD=BD，所以△ACD≌△EBD（__________).

    所以BE=AC(_____________________).

    因为AB+BE>AE(_____________________)，

    所以AB+AC>AE.

    因为AE=2AD=8cm，

    所以AB+AC>_______cm.

    【答案】答案见解析

    【解析】

    根据三角形全等的判定与性质以及三角形的内角和，即可得出答案.

    解：延长AD到E,使DE = AD,连接BE.

    因为AD为△ABC的中线，

    所以BD=CD.

    在△ACD和△EBD中，因为AD=DE,∠ADC=∠EDB,CD=BD，所以△ACD≌△EBD（SAS).

    所以BE=AC(全等三角形的性质).

    因为AB+BE>AE(两边之和大于第三边)，

    所以AB+AC>AE.

    因为AE=2AD=8cm，

    所以AB+AC>8cm.

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    【题目】某中学开展以“我最喜爱的传统文化”为主题的调查活动，从“诗词、国画、对联、书法、戏曲”五种传统文化中，选取喜欢的一种（只选一种）进行调查，将调查结果整理后绘制成如图所示的不完整统计图.

    （1）本次调查共抽取了多少名学生？

    （2）喜欢“书法”的有多少名学生？并补全条形统计图；

    （3）求喜欢“国画”对应扇形圆心角的度数.

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】某电器商场销售A、B两种型号计算器，两种计算器的进货价格分别为每台30元，40元，商场销售5台A型号和1台B型号计算器，可获利润76元；销售6台A型号和3台B型号计算器，可获利润120元．求商场销售A、B两种型号计算器的销售价格分别是多少元？（利润=销售价格﹣进货价格）

    查看答案和解析>>

    科目：初中数学 来源： 题型：

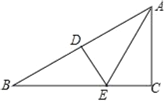
    【题目】如图，在△ABC中，∠B＝30°，边AB的垂直平分线分别交AB和BC于点D，E，且AE平分∠BAC．

    （1）求∠C的度数；

    （2）若CE＝1，求AB的长．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】某电视台的一档娱乐性节目中，在游戏PK环节，为了随机分选游戏双方的组员，主持人设计了以下游戏：用不透明的白布包住三根颜色长短相同的细绳AA1、BB1、CC1，只露出它们的头和尾（如图所示），由甲、乙两位嘉宾分别从白布两端各选一根细绳，并拉出，若两人选中同一根细绳，则两人同队，否则互为反方队员．

    （1）若甲嘉宾从中任意选择一根细绳拉出，求他恰好抽出细绳AA1的概率；

    （2）请用画树状图法或列表法，求甲、乙两位嘉宾能分为同队的概率．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，在Rt△ABC中，∠C=90°，以AC为直径作⊙O，交AB于D，过点O作OE∥AB，交BC于E．

    （1）求证：ED为⊙O的切线；

    （2）如果⊙O的半径为，ED=2，延长EO交⊙O于F，连接DF、AF，求△ADF的面积．

    【答案】（1）证明见解析；（2）

    【解析】试题分析：（1）首先连接OD，由OE∥AB，根据平行线与等腰三角形的性质，易证得≌ 即可得，则可证得为的切线；
    （2）连接CD，根据直径所对的圆周角是直角，即可得 利用勾股定理即可求得的长，又由OE∥AB，证得根据相似三角形的对应边成比例，即可求得的长，然后利用三角函数的知识，求得与的长，然后利用S△ADF=S梯形ABEF-S梯形DBEF求得答案．

    试题解析：(1)证明：连接OD，

    ∵OE∥AB，

    ∴∠COE=∠CAD，∠EOD=∠ODA，

    ∵OA=OD,

    ∴∠OAD=∠ODA，

    ∴∠COE=∠DOE，

    在△COE和△DOE中，

    ∴△COE≌△DOE(SAS)，

    ∴ED⊥OD，

    ∴ED是的切线；

    (2)连接CD，交OE于M，

    在Rt△ODE中，

    ∵OD=32，DE=2，

    ∵OE∥AB，

    ∴△COE∽△CAB，

    ∴AB=5，

    ∵AC是直径，

    ∵EF∥AB，

    ∴S△ADF=S梯形ABEFS梯形DBEF

    ∴△ADF的面积为

    【题型】解答题
    【结束】
    25

    【题目】【题目】已知，抛物线y=ax2+ax+b（a≠0）与直线y=2x+m有一个公共点M（1，0），且a＜b．

    （1）求b与a的关系式和抛物线的顶点D坐标（用a的代数式表示）；

    （2）直线与抛物线的另外一个交点记为N，求△DMN的面积与a的关系式；

    （3）a=﹣1时，直线y=﹣2x与抛物线在第二象限交于点G，点G、H关于原点对称，现将线段GH沿y轴向上平移t个单位（t＞0），若线段GH与抛物线有两个不同的公共点，试求t的取值范围．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

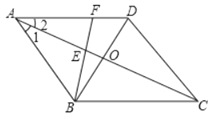
    【题目】如图，已知□ABCD的对角线AC、BD交于O，且∠1=∠2．

    （1）求证：□ABCD是菱形；

    （2）F为AD上一点,连结BF交AC于E,且AE=AF.求证：AO=（AF+AB）．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

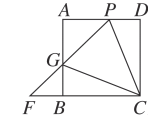
    【题目】(1)如图，正方形ABCD中，∠PCG＝45°，且PD＝BG，求证：FP＝FC.

    (2)如图，正方形ABCD中，∠PCG＝45°，延长PG交CB的延长线于点F，(1)中的结论还成立吗？请说明理由．

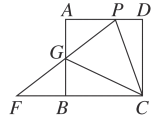
    (3)在(2)的条件下，作FE⊥PC，垂足为E，交CG于点N，连接DN，求∠NDC的度数．

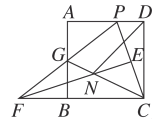
    查看答案和解析>>

    科目：初中数学 来源： 题型：

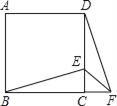
    【题目】如图，正方形ABCD中，E为CD上一点，F为BC延长线上一点，CE=CF．

    （1）△DCF可以看作是△BCE绕点C旋转某个角度得到的吗？

    （2）若∠CEB=60°，求∠EFD的度数．

    查看答案和解析>>

    同步练习册答案