
【题目】在四边形ABCD中,有下列条件:①![]() ;②
;②![]() ;③AC=BD;④AC⊥BD.
;③AC=BD;④AC⊥BD.
(1)从中任选一个作为已知条件,能判定四边形ABCD是平行四边形的概率是 ;
(2)从中任选两个作为已知条件,请用画树状图法求出能判定四边形ABCD是矩形的概率,并判断能判定四边形ABCD是矩形和是菱形的概率是否相等?
【答案】(1)![]() ;(2)四边形ABCD是矩形和是菱形的概率相等.理由见解析.
;(2)四边形ABCD是矩形和是菱形的概率相等.理由见解析.
【解析】
(1)根据概率即可得到结论;
(2)列表得出所有等可能的情况数,找出能判定四边形ABCD是矩形和菱形的情况数,即可求出所求的概率.
(1)选①或②能判定四边形ABCD是平行四边形,
故概率=![]() =
=![]() ;
;
(2)从中任选两个作为已知条件,请用画树状图法求出能判定四边形ABCD是矩形的概率,并判断能判定四边形ABCD是矩形和是菱形的概率是否相等?
解:画树状图如下:

由树状图可知,共有12种等可能结果,能判定四边形ABCD是矩形的有4种,即①③、③①、②③、③②;能判定四边形ABCD是菱形的有4种,①④、④①、②④、④②;
∴能判定四边形ABCD是矩形的概率为![]() =
=![]() ,
,
能判定四边形ABCD是菱形的概率为![]() =
=![]() .
.
∴四边形ABCD是矩形和是菱形的概率相等.


科目:初中数学 来源: 题型:
【题目】某服装店出售某品牌的棉衣,进价为100元/件,当售价为150元/件时,平均每天可卖30件;为了增加利润和减少库存,商店决定降价销售.经调査,每件每降价1元,则每天可多卖2件.
(1)若每件降价20元,则平均每天可卖______件.
(2)现要想平均每天获利2000元,且让顾客得到实惠,求每件棉衣应降价多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】襄阳市精准扶贫工作已进入攻坚阶段.贫困户张大爷在某单位的帮扶下,把一片坡地改造后种植了优质水果蓝莓,今年正式上市销售.在销售的30天中,第一天卖出20千克,为了扩大销量,采取了降价措施,以后每天比前一天多卖出4千克.第x天的售价为y元/千克,y关于x的函数解析式为![]() 且第12天的售价为32元/千克,第26天的售价为25元/千克.已知种植销售蓝莓的成木是18元/千克,每天的利润是W元(利润=销售收入﹣成本).
且第12天的售价为32元/千克,第26天的售价为25元/千克.已知种植销售蓝莓的成木是18元/千克,每天的利润是W元(利润=销售收入﹣成本).
(1)m= ,n= ;
(2)求销售蓝莓第几天时,当天的利润最大?最大利润是多少?
(3)在销售蓝莓的30天中,当天利润不低于870元的共有多少天?
查看答案和解析>>
科目:初中数学 来源: 题型:
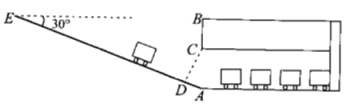
【题目】如下图,从地面E点测得地下停车场的俯角为30°,斜坡AE的长为16米.地面B点(与E点在同一个水平线)距停车场顶部C点(A、C、B在同一条直线上且与水平线垂直)1.2米.试求该校地下停车场的高度AC及限高CD(结果精确到0.1米,![]() ).
).
查看答案和解析>>
科目:初中数学 来源: 题型:
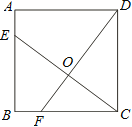
【题目】如图,已知正方形ABCD的边长为4,点E、F分别在边AB、BC上,且AE=BF=1,CE、DF交于点O.下列结论:①∠DOC=90°, ②OC=OE, ③tan∠OCD =![]() ,④
,④![]() 中,正确的有( )
中,正确的有( )
A.1个B.2个C.3个D.4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线![]() 与x轴交于点
与x轴交于点![]() ,点
,点![]() ,与y轴交于点C,且过点
,与y轴交于点C,且过点![]() .点P、Q是抛物线
.点P、Q是抛物线![]() 上的动点.
上的动点.
(1)求抛物线的解析式;
(2)当点P在直线OD下方时,求![]() 面积的最大值.
面积的最大值.
(3)直线OQ与线段BC相交于点E,当![]() 与
与![]() 相似时,求点Q的坐标.
相似时,求点Q的坐标.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】学校准备在各班设立图书角以丰富同学们的课余文化生话.为了更合理的搭配各类书籍,学校团委以“我最喜爱的书籍”为主题,对学生最喜爱的一种书籍类型进行随机抽样调查,收集整理数据后,绘制出以下两幅未完成的统计图,请根据图①和图②提供的信息,解答下列问题:
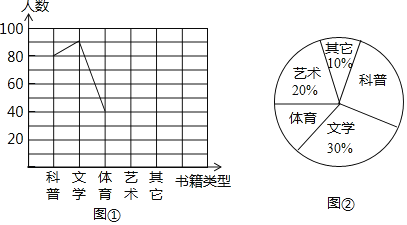
(1)在这次抽样调查中,一共调查了多少名学生?
(2)请把折线统计图补充完整;
(3)学校若在喜爱艺术、文学、科普、体育四类中任意选取两类建立兴趣小姐.请用列表或画树状图的方法求出恰好选中体育和科普两类的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,抛物线![]() 与
与![]() 轴交于点
轴交于点![]() 和
和![]() ,与
,与![]() 轴交于点
轴交于点![]() .
.
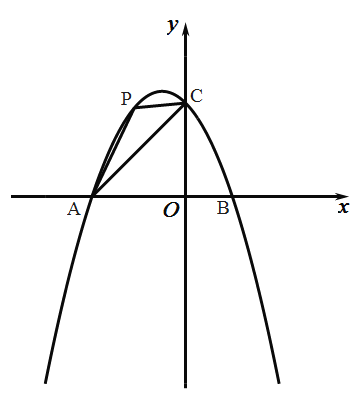
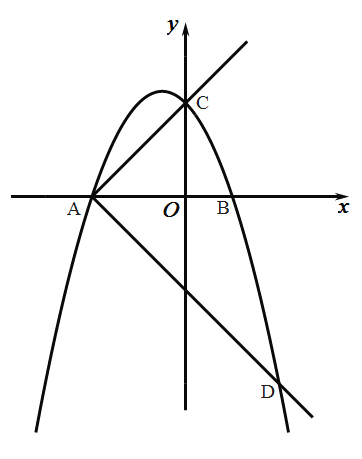
(1)求抛物线的表达式;
(2)点![]() 是抛物线上第二象限内的点,连接
是抛物线上第二象限内的点,连接![]() ,设
,设![]() 的面积为
的面积为![]() ,当
,当![]() 取最大值时,求点
取最大值时,求点![]() 的坐标;
的坐标;
(3)作射线![]() ,将射线
,将射线![]() 绕
绕![]() 点顺时针旋转
点顺时针旋转![]() 交抛物线于另一点
交抛物线于另一点![]() ,在射线
,在射线![]() 上是否存在一点
上是否存在一点![]() ,使
,使![]() 的周长最小.若存在,求出
的周长最小.若存在,求出![]() 的坐标;若不存在,请说明理由.
的坐标;若不存在,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com