
【题目】![]() 如图
如图![]() ,线段
,线段![]() ,
,![]() ,点
,点![]() 从点
从点![]() 开始绕着点
开始绕着点![]() 以
以![]() 的速度顺时针旋转一周回到点
的速度顺时针旋转一周回到点![]() 后停止,点
后停止,点![]() 同时出发沿射线
同时出发沿射线![]() 自
自![]() 点向
点向![]() 点运动,若点
点运动,若点![]() 、
、![]() 两点能恰好相遇,则点
两点能恰好相遇,则点![]() 运动的速度为________
运动的速度为________![]() ;
;

![]() 将一副三角板中的两块直角三角尺的直角顶点
将一副三角板中的两块直角三角尺的直角顶点![]() 按如图方式叠放在一起(其中,
按如图方式叠放在一起(其中,![]() ,
,![]() ,
,![]() ;
;![]() ).将三角尺
).将三角尺![]() 固定,另一三角尺
固定,另一三角尺![]() 的
的![]() 边从
边从![]() 边开始绕点
边开始绕点![]() 转动,转动速度与
转动,转动速度与![]() 问中
问中![]() 点速度相同,当
点速度相同,当![]() 且点
且点![]() 在直线
在直线![]() 的上方时,这两块三角尺是否存在一组边互相平行?若存在,请写出
的上方时,这两块三角尺是否存在一组边互相平行?若存在,请写出![]() 有可能的值及对应转动的时间;若不存在,请说明理由.
有可能的值及对应转动的时间;若不存在,请说明理由.
【答案】(1)![]() 或
或![]() ;(2)详见解析.
;(2)详见解析.
【解析】
(1)求出点P到达点G和回到点M的时间,再根据点P、Q相遇的地点只有G、M,利用速度=路程÷时间列式计算即可得解;
(2)根据平行线的性质,按照旋转角从小到大的顺序依次确定出有两边平行时的旋转角,再求出时间即可.
解:(1)∵点P在⊙O上绕点O旋转的速度为15°/s,
∴点P到达点G的时间为180°÷15°=12s,
回到点M的时间为360°÷15°=24s,
∵点Q在射线NM上运动,
∴点P、Q相遇的地点只有G、M,
∴点Q运动的速度为(30-3×2)÷12=2cm/s,
或30÷24=1.25cm/s,
故答案为:![]() 或
或![]() ;
;
![]() 存在,
存在,
当![]() 时,
时,![]() ,用时
,用时![]() ,
,
当![]() 时,
时,![]() ,用时
,用时![]() ,
,
当![]() 时,
时,![]() ,用时
,用时![]() ,
,
当![]() 时,
时,![]() ,用时
,用时![]() ,
,
当![]() 时,
时,![]() ,用时
,用时![]() .
.


科目:初中数学 来源: 题型:
【题目】阅读下面材料:
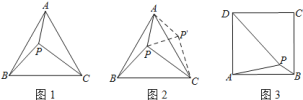
小伟遇到这样一个问题:如图![]() ,在正三角形
,在正三角形![]() 内有一点
内有一点![]() ,且
,且![]() ,
,![]() ,
,![]() ,求
,求![]() 的度数.小伟是这样思考的:如图
的度数.小伟是这样思考的:如图![]() ,利用旋转和全等的知识构造
,利用旋转和全等的知识构造![]() ,连接
,连接![]() ,得到两个特殊的三角形,从而将问题解决.
,得到两个特殊的三角形,从而将问题解决.
(1)请你回答:图![]() 中
中![]() 的度数等于________.
的度数等于________.
参考小伟同学思考问题的方法,解决下列问题:
(2)如图![]() ,在正方形
,在正方形![]() 内有一点
内有一点![]() ,且
,且![]() ,
,![]() ,
,![]() ,求
,求![]() 的度数和正方形的边长.
的度数和正方形的边长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】九年级(1)班全班50名同学组成五个不同的兴趣爱好小组,每人都参加且只能参加一个小组,统计(不完全)人数如下表:
编号 | 一 | 二 | 三 | 四 | 五 |
人数 |
| 15 | 20 | 10 |
|
已知前面两个小组的人数之比是![]() .
.
解答下列问题:
(1)![]() .
.
(2)补全条形统计图:
(3)若从第一组和第五组中任选两名同学,求这两名同学是同一组的概率.(用树状图或列表把所有可能都列出来)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一辆货车早晨7∶00出发,从甲地驶往乙地送货.如图是货车行驶路程y(km)与行驶时间x(h)的完整的函数图像(其中点B、C、D在同一条直线上),小明研究图像得到了以下结论:
①甲乙两地之间的路程是100 km;
②前半个小时,货车的平均速度是40 km/h;
③8∶00时,货车已行驶的路程是60 km;
④最后40 km货车行驶的平均速度是100 km/h;
⑤货车到达乙地的时间是8∶24,
其中,正确的结论是( )

A.①②③④B.①③⑤C.①③④D.①③④⑤
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,分别以Rt△ABC的直角边AC、BC为边,在Rt△ABC外作两个等边三角形△ACE和△BCF,连接BE、AF分别交AC、BC边于H、D两点.下列结论:①AF=BE;②∠AFC=∠EBC;③∠FAE=90°;④BD=FD,其中正确结论的个数是( )

A.4个B.3个C.2个D.1个
查看答案和解析>>
科目:初中数学 来源: 题型:
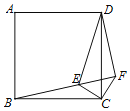
【题目】如图,在正方形ABCD内一点E连接BE、CE,过C作CF⊥CE与BE延长线交于点F,连接DF、DE.CE=CF=1,DE=![]() ,下列结论中:①△CBE≌△CDF;②BF⊥DF;③点D到CF的距离为2;④S四边形DECF=
,下列结论中:①△CBE≌△CDF;②BF⊥DF;③点D到CF的距离为2;④S四边形DECF=![]() +1.其中正确结论的个数是( )
+1.其中正确结论的个数是( )
A.1B.2C.3D.4
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图(1),有A、B、C三种不同型号的卡片若干张,其中A型是边长为a(a>b)的正方形,B型是长为a、宽为b的长方形,C型是边长为b的正方形.

(1)若用A型卡片1张,B型卡片2张,C型卡片1张拼成了一个正方形(如图(2)),此正方形的边长为 ,根据该图形请写出一条属于因式分解的等式: .
(2)若要拼一个长为2a+b,宽为a+2b的长方形,设需要A类卡片x张,B类卡片y张,C类卡片z张,则x+y+z= .
(3)现有A型卡片1张,B型卡片6张,C型卡片11张,从这18张卡片中拿掉两张卡片,余下的卡片全用上,你能拼出一个长方形或正方形吗?有几种拼法?请你通过运算说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com