Question

8．如图，点A在反比例函数y=$\frac{1}{x}$（x＞0）的图象上，点B在反比例函数y=-$\frac{3}{x}$（x＜0）的图象上，且OA⊥OB．线段AB交反比例函数y=$\frac{1}{x}$（x＞0）的图象于另一点C，连接OC，若点C为AB的中点，则tan∠OCA的值为$\sqrt{3}$．

Answer 1

分析 过点A作AD⊥x轴于点D，过点B作BE⊥x轴于点E，则△AOD∽△OBE，设点A的坐标为（m，$\frac{1}{m}$），点B的坐标为（n，-$\frac{3}{n}$），根据点C为AB的中点即可找出点C的坐标，再结合相似三角形的性质即可得出m、n的关系，结合点在反比例函数的性质即可得出关于m、n的二元二次方程，解方程组求出m、n的值，进而即可得出点A、B的坐标，利用正切的定义结合等边三角形的判定即可得出△AOC为等边三角形，由此即可得出结论．

解答 解：过点A作AD⊥x轴于点D，过点B作BE⊥x轴于点E，则△AOD∽△OBE，如图所示．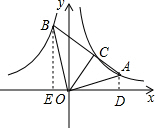
设点A的坐标为（m，$\frac{1}{m}$），点B的坐标为（n，-$\frac{3}{n}$），
∵点C为AB的中点，
∴C（$\frac{m+n}{2}$，$\frac{\frac{1}{m}-\frac{3}{n}}{2}$）．
∵△AOD∽△OBE，
∴$\frac{-n}{\frac{1}{m}}=\frac{-\frac{3}{n}}{m}$，即m²n²=3①．
∵点C在反比例函数y=$\frac{1}{x}$（x＞0）的图象上，
∴$\frac{m+n}{2}$•$\frac{\frac{1}{m}-\frac{3}{n}}{2}$=1，即6mn=-3m²+n²②．
联立①②成方程组，解得：$\left\{\begin{array}{l}{m=\frac{\sqrt{6}+\sqrt{2}}{2}}\\{n=\frac{\sqrt{6}-3\sqrt{2}}{2}}\end{array}\right.$或$\left\{\begin{array}{l}{m=-\frac{\sqrt{6}+\sqrt{2}}{2}}\\{n=\frac{3\sqrt{2}-\sqrt{6}}{2}}\end{array}\right.$（舍去），
∴A（$\frac{\sqrt{6}+\sqrt{2}}{2}$，$\frac{\sqrt{6}-\sqrt{2}}{2}$），B（$\frac{\sqrt{6}-3\sqrt{2}}{2}$，$\frac{\sqrt{6}+3\sqrt{2}}{2}$），
∴OA=2，OB=2$\sqrt{3}$．
在Rt△AOB中，OA=2，OB=2$\sqrt{3}$，∠AOB=90°，
∴tan∠BAO=$\frac{OB}{OA}$=$\sqrt{3}$，
∴∠BAO=60°，
∵OC是△AOB的中位线，
∴OC=$\frac{1}{2}$AB=AC，
∴△AOC为等边三角形，
∴∠OCA=60°，tan∠OCA=$\sqrt{3}$，
故答案为：$\sqrt{3}$．

点评 本题考查了相似三角形的性质、反比例函数图象上点的坐标特征以及等边三角形的判定，解题的关键是找出△AOC为等边三角形．本题属于中档题，难度不大，解决该题型题目时，根据反比例函数图象上点的坐标特征以及相似三角形的性质得出方程组是关键．