
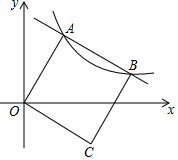
 如图,平面直角坐标系中,O为坐标原点,正方形OABC的顶点A,B都在反比例函数y=$\frac{k}{x}$(k>0,x>0)的图象上,边BC与x轴交于点D,则$\frac{BD}{CD}$的值为$\frac{\sqrt{5}-1}{2}$.
如图,平面直角坐标系中,O为坐标原点,正方形OABC的顶点A,B都在反比例函数y=$\frac{k}{x}$(k>0,x>0)的图象上,边BC与x轴交于点D,则$\frac{BD}{CD}$的值为$\frac{\sqrt{5}-1}{2}$. 分析 过A作AE⊥x轴于E,过B作BF⊥x轴于F,BG⊥AE于G,于是得到EF=BG,BF=GE,根据正方形的性质得到OA=AB,∠OAB=90°,根据余角的性质得到∠OAE=∠ABG,根据全等三角形的性质得到AG=OE,AE=BG,设A(a,$\frac{k}{a}$),得到OE=AG=a,AE=BG=$\frac{k}{a}$,求得B($\frac{k}{a}$+a,$\frac{k}{a}$-a),得方程求得k=$\frac{\sqrt{5}+1}{2}$a2(负值舍去),过C作CH⊥x轴于H,根据相似三角形的性质即可得到结论.
解答 解:过A作AE⊥x轴于E,过B作BF⊥x轴于F,BG⊥AE于G,
则EF=BG,BF=GE,
∵四边形OABC是正方形,
∴OA=AB,∠OAB=90°,
∴∠OAE+∠BAE=∠BAE+∠ABG=90°,
∴∠OAE=∠ABG,
在△AOE与△BAG中,$\left\{\begin{array}{l}{∠OAE=∠ABG}\\{∠AEO=∠AGB}\\{OA=AB}\end{array}\right.$,
∴△AOE≌△BAG,
∴AG=OE,AE=BG,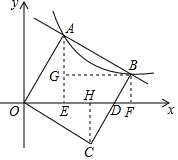
设A(a,$\frac{k}{a}$),
∴OE=AG=a,AE=BG=$\frac{k}{a}$,
∴B($\frac{k}{a}$+a,$\frac{k}{a}$-a),
∴($\frac{k}{a}$+a)($\frac{k}{a}$-a)=k,
解得k=$\frac{\sqrt{5}+1}{2}$a2(负值舍去),
∴B点的纵坐标为$\frac{\sqrt{5}-1}{2}a$,
BF=$\frac{\sqrt{5}-1}{2}$a,
过C作CH⊥x轴于H,
同理△AOE≌△OCH,
∴CH=OE=a,
∵CH⊥x轴,BF⊥x轴,
∴CH∥BF,
∴△BFD∽△CHD,
∴$\frac{BD}{CD}$=$\frac{BF}{CH}$=$\frac{\frac{\sqrt{5}-1}{2}a}{a}$=$\frac{\sqrt{5}-1}{2}$,
故答案为:$\frac{\sqrt{5}-1}{2}$.
点评 本题考查了反比例函数的系数k的几何意义,正方形的性质,全等三角形的判定与性质,相似三角形的判定和性质,正确的作出辅助线是解题的关键.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:填空题

查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 210x+90(18-x)≥2100 | B. | 90x+210(18-x)≤2100 | ||
| C. | 210x+90(18-x)≥2.1 | D. | 210x+90(18-x)>2.1 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
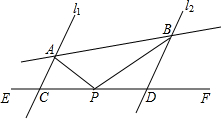 如图,已知直线l1∥l2,直线AB与l1,l2分别交于点A,B,直线EF与l1,l2分别交于点C,D,P是直线EF上的任意一点(不与点C,D重合).
如图,已知直线l1∥l2,直线AB与l1,l2分别交于点A,B,直线EF与l1,l2分别交于点C,D,P是直线EF上的任意一点(不与点C,D重合).查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 如图,在平面直角坐标系中,OB=OA=6,OC=12,点P从A出发运动到C点,将BP绕P顺时针旋转90°得到点Q,求在整个运动的过程中,Q点滑过的长度为6$\sqrt{2}$.
如图,在平面直角坐标系中,OB=OA=6,OC=12,点P从A出发运动到C点,将BP绕P顺时针旋转90°得到点Q,求在整个运动的过程中,Q点滑过的长度为6$\sqrt{2}$.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com