
如图,在△ABC中,AB=AC, 点M在△ABC内,点P在线段MC上,∠ABP=2∠ACM.

(1)若∠PBC=10°,∠BAC=80°,求∠MPB的值
(2)若点M在底边BC的中线上,且BP=AC,试探究∠A与∠ABP之间的数量关系,并证明.
(1) ∠MPB=40°;(2) ∠BAC+∠ABP=120°.证明见解析 【解析】试题分析:(1)由AB=AC,∠BAC=80°,可求∠ABC=∠ACB=50°,又∠PBC=10°,∠ABP=2∠ACM,可求∠BCM=30°,由三角形外角的性质可求出结果; (2)过点A作底边BC的中线AD,连接BM,由等腰三角形三线合一的性质可得∠CAM=∠BAM,从而可证△ABM≌△ACM.进而证... 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源:江苏省无锡市2017-2018学年七年级上学期期末考试数学试卷 题型:解答题
计算:
(1) (-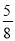 -
-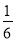 +
+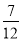 )×24+5; (2)-32-(1-
)×24+5; (2)-32-(1-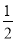 )÷3×|3-(-3)2|.
)÷3×|3-(-3)2|.
查看答案和解析>>
科目:初中数学 来源:湖北省襄阳市襄城区2017-2018学年七年级上学期期末考试数学试卷 题型:单选题
若关于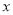 的方程
的方程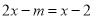 的解为
的解为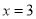 ,则
,则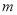 的值为( )
的值为( )
A. -5 B. 5 C. -7 D. 7
B 【解析】试题解析:把x=3代入方程得:6-m=3-2, 解得:m=5, 故选B.查看答案和解析>>
科目:初中数学 来源:江苏省泰兴市2017-2018学年八年级上学期期末考试数学试卷 题型:填空题
请写出一个经过点(-1,2)且y随x的增大而减小的一次函数表达式 __________.
略 【解析】试题解析:∵随的增大而减小, 不妨设为 把(?1,2)代入得, 解得 ∴函数解析式为 故答案为: (答案不唯一).查看答案和解析>>
科目:初中数学 来源:江苏省泰兴市2017-2018学年八年级上学期期末考试数学试卷 题型:单选题
如图,数轴上的点A表示的数是-1,点B表示的数是1,CB⊥AB于点B,且BC=2,以点A为圆心,AC为半径画弧交数轴于点D,则点D表示的数为( )
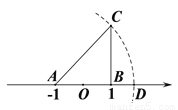
A. 2.8 B. 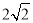 C.
C.  -
-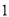 D.
D. 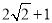
查看答案和解析>>
科目:初中数学 来源:2017-2018年福建厦门市八年级上册数学期末质量检测试卷 题型:解答题
计算: (x+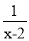 )·
)·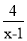 -3.
-3.
查看答案和解析>>
科目:初中数学 来源:2017-2018年福建厦门市八年级上册数学期末质量检测试卷 题型:填空题
已知△ABC是等腰三角形,∠A是底角,若∠A=70°,则∠B=_______.
70°或40°. 【解析】试题解析:∵∠A是底角,若∠A=70°,△ABC是等腰三角形, ∴分二种情况; ①当∠B为底角时,∠B=∠A=70°; ②当∠B为顶角时,∠B=180°-70°×2=40°. 故答案为:70°或40°.查看答案和解析>>
科目:初中数学 来源:河北省唐山市路北区2017-2018学年度第一学期学生素质终期评价九年级数学 题型:解答题
如图,四边形ABCD内接于⊙O,对角线AC为⊙O的直径,过点C作AC的垂线交AD的延长线于点E,点F为CE的中点,连接DB,DF
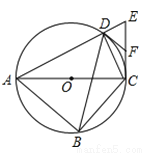
(1)求∠CDE的度数
(2)求证:DF是⊙O的切线
证明见解析 【解析】试题分析:(1)直接利用圆周角定理得出∠CDE的度数; (2)直接利用直角三角形的性质结合等腰三角形的性质得出∠ODF=∠ODC+∠FDC=∠OCD+∠DCF=90°,进而得出答案. 试题解析:(1)∵对角线AC为⊙O的直径, ∴∠ADC=90°, ∴∠EDC=90°; (2)连接DO, ∵∠EDC=90°,F是EC的中点,∴DF=FC...查看答案和解析>>
科目:初中数学 来源:广东省深圳市龙岗区2017-2018学年度第一学期期末质量检测八年级数学试卷 题型:单选题
如图,在数轴上表示实数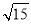 的点可能是( )
的点可能是( )
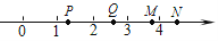
A. 点P B. 点Q C. 点M D. 点N
C 【解析】试题分析:因为,则,即处在3和4之间,即点M可能为.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com