
【题目】如图,正六边形OABCDE中,点E(﹣2,0),将该正六边形向右平移a(a>0)个单位后,恰有两个顶点落在反比例函数y=![]() (k>0)的图象上,则k的值为__.
(k>0)的图象上,则k的值为__.

【答案】2![]() 或6
或6![]()
【解析】
根据题意可以分别求得点A、B、C对应的点的坐标,然后根据题意可知反比例函数可能经过点A和点B的对应点或经过点A和点C的对应点,从而可以求得k的值.
由题意可得:∠AOE=120°,OE=OA=2,∴点A的坐标为(1,![]() ),点B的坐标为(0,2
),点B的坐标为(0,2![]() ),点C(﹣2,2
),点C(﹣2,2![]() ),将该正六边形向右平移a(a>0)个单位后点A对应的点的坐标为(1+a,
),将该正六边形向右平移a(a>0)个单位后点A对应的点的坐标为(1+a,![]() ),点B对应的点的坐标为(a,2
),点B对应的点的坐标为(a,2![]() ),点C对应的点的坐标为(﹣2+a,2
),点C对应的点的坐标为(﹣2+a,2![]() ).
).
①当平移后点A的对应点和点B的对应点在反比例函数y=![]() (k>0)的图象上时,(1+a)
(k>0)的图象上时,(1+a)![]() =a
=a![]() ,解得:a=1,则k=(1+a)
,解得:a=1,则k=(1+a)![]() =2
=2![]() .
.
②当平移后点A的对应点和点C的对应点在反比例函数y=![]() (k>0)的图象上时,(1+a)
(k>0)的图象上时,(1+a)![]() =(﹣2+a)
=(﹣2+a)![]() ,得:a=5,k=(1+a)
,得:a=5,k=(1+a)![]() =6
=6![]() .
.
故答案为:2![]() 或6
或6![]() .
.


 课程达标测试卷闯关100分系列答案
课程达标测试卷闯关100分系列答案 新卷王期末冲刺100分系列答案
新卷王期末冲刺100分系列答案 全能闯关100分系列答案
全能闯关100分系列答案科目:初中数学 来源: 题型:
【题目】如图1,甲、乙两个容器内都装了一定数量的水,现将甲容器中的水匀速注入乙容器中.图2中的线段AB,CD分别表示容器中的水的深度h(厘米)与注入时间t(分钟)之间的函数图象.下列结论错误的是( )
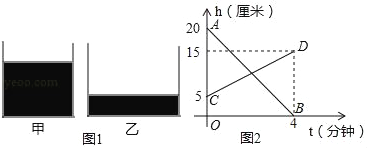
A. 注水前乙容器内水的高度是5厘米
B. 甲容器内的水4分钟全部注入乙容器
C. 注水2分钟时,甲、乙两个容器中的水的深度相等
D. 注水1分钟时,甲容器的水比乙容器的水深5厘米
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直线y=![]() x+4与x轴相交于点A,与y轴相交于点B.
x+4与x轴相交于点A,与y轴相交于点B.

(1)求△AOB的面积;
(2)过B点作直线BC与x轴相交于点C,若△ABC的面积是16,求点C的坐标;
(3)若P是坐标轴上一点,且PA=PB,求P的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知,等腰Rt△OAB中,∠AOB=90°,等腰Rt△EOF中,∠EOF=90°,连结AE、BF.

求证:(1)AE=BF;(2)AE⊥BF.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知![]() 中,
中,![]() ,
,![]() 分别平分
分别平分![]() 和
和![]() ,
,![]() 、
、![]() 交于点
交于点![]() .
.

(1)直接写出![]() 与
与![]() 的数量关系;
的数量关系;
(2)若![]() ,利用(1)的关系,求出
,利用(1)的关系,求出![]() 的度数;
的度数;
(3)利用(2)的结果,试判断![]() 、
、![]() 、
、![]() 的数量关系,并证明.
的数量关系,并证明.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,平面直角坐标系中,△ABC三个顶点的坐标分别为A(1,0),B(2,-3),C(4,-2).
(1)在图中作出△ABC关于x轴对称的图形△A1B1C1.
(2)作出△A1B1C1向左平移4个单位长度后得到的△A2B2C2,并直接写出点C2的坐标_____.
(3)△A2B2C2的面积是____.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,等腰Rt△ABC中,∠ABC=90°,点A,B分别在坐标轴上.
(1)如图①,若点C的横坐标为5,求点B的坐标.
(2)如图②,若BC交x轴于M,过C作CD⊥BC交y轴于D . 求证:BC-CD=MC.
(3)如图③,若点A的坐标为(-4,0),点B是y轴正半轴上的一个动点,分别以OB,AB为直角边在第一、第二象限作等腰Rt△OBF(∠OBF=90°)、等腰Rt△ABE(∠ABE=90°),连接EF交y轴于点P,当点B在y轴上运动时,PB的长度是否发生改变?若不变,求出PB的值;若变化,求PB的取值范围.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在四边形ABCD中,AB∥CD,∠1=∠2,DB=DC.
(1)求证:△ABD≌△EDC;
(2)若∠A=135°,∠BDC=30°,求∠BCE的度数.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】计算
我区在一项工程招标时,接到甲、乙两个工程队的投标书,从投标书中得知:每施工一天,甲工程队要![]() 万元,乙工程队要
万元,乙工程队要![]() 万元,工程小组根据甲、乙两队标书的测算,有三种方案:
万元,工程小组根据甲、乙两队标书的测算,有三种方案:![]() 甲队单独完成这个工程,刚好如期完成;
甲队单独完成这个工程,刚好如期完成;![]() 乙队单独完成这个工程要比规定时间多用5天;
乙队单独完成这个工程要比规定时间多用5天;![]() **********,剩下的工程由乙队单独做,也正好如期完成. 方案
**********,剩下的工程由乙队单独做,也正好如期完成. 方案![]() 中“星号”部分被损毁了. 已知,一个同学设规定的工期为
中“星号”部分被损毁了. 已知,一个同学设规定的工期为![]() 天,根据题意列出方程:
天,根据题意列出方程:![]()
(1)请将方案中“星号”部分补充出来________________;
(2)你认为哪个方案节省工程款,请说明你的理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com