
【题目】如图,在菱形ABCD中,对角线AC、BD交于点O,以OB为直径画圆M,过D作⊙M的切线,切点为N,分别交AC、BC于点E、F,已知AE=5,CE=3,则DF的长是( ) 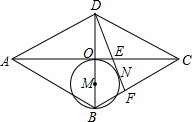
A.3
B.4
C.4.8
D.5
【答案】C
【解析】解:延长EF,过点B作直线平行AC和EF相交于P, ∵AE=5,EC=3,
∴AC=AE+CE=8,
∵四边形ABCD是菱形,
∴OA=OC= ![]() AC=4,AC⊥BD,
AC=4,AC⊥BD,
∴OE=OC﹣CE=4﹣3=1,
∵以OB为直径画圆M,
∴AC是⊙M的切线,
∵DN是⊙M的切线,
∴EN=OE=1,MN⊥AN,
∴∠DNM=∠DOE=90°,
∵∠MDN=∠EDO,
∴△DMN∽△DEO,
∴DM:MN=DE:OE,
∵MN=BM=OM= ![]() OB,
OB,
∴DM=OD+OM=3MN,
∴DE=3OE=3,
∵OE∥BP,
∴OD:OB=DE:EP,
∵OD=OB,
∴DE=EP=3,
∴BP=2OE=2,
∵OE∥BP,
∴△EFC∽△PFB,
∴EF:PF=EC:BP=3:2,
∴EF:EP=3:5,
∴EF=EP× ![]() =1.8,
=1.8,
∴DF=DE+EF=3+1.8=4.8.
故选C.


科目:初中数学 来源: 题型:
【题目】如图,网格线的交点叫格点,格点![]() 是
是![]() 的边
的边![]() 上的一点(请利用网格作图,保留作图痕迹).
上的一点(请利用网格作图,保留作图痕迹).

(1)过点![]() 画
画![]() 的垂线,交
的垂线,交![]() 于点
于点![]() ;
;
(2)线段 的长度是点O到PC的距离;
(3)![]() 的理由是 ;
的理由是 ;
(4)过点C画![]() 的平行线;
的平行线;
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我们把形如x2=a(其中a是常数且a≥0)这样的方程叫做x的完全平方方程.
如x2=9,(3x﹣2)2=25,![]() …都是完全平方方程.
…都是完全平方方程.
那么如何求解完全平方方程呢?
探究思路:
我们可以利用“乘方运算”把二次方程转化为一次方程进行求解.
如:解完全平方方程x2=9的思路是:由(+3)2=9,(﹣3)2=9可得x1=3,x2=﹣3.
解决问题:
(1)解方程:(3x﹣2)2=25.
解题思路:我们只要把 3x﹣2 看成一个整体就可以利用乘方运算进一步求解方程了.
解:根据乘方运算,得3x﹣2=5 或 3x﹣2= .
分别解这两个一元一次方程,得x1=![]() ,x2=﹣1.
,x2=﹣1.
(2)解方程![]() .
.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知数轴上点A表示的数为10,点B在点A左边,且AB=18.动点P从点A出发,以每秒5个单位长度的速度沿数轴向左匀速运动,设运动时间为t(t>0)秒.
(1)写出数轴上点B表示的数,点P表示的数(用含t的代数式表示);
(2)动点Q从点B出发,以每秒3个单位长度的速度沿数轴向左匀速运动,若点P、Q同时出发.
①问点P运动多少秒时追上点Q?
②问点P运动多少秒时与点Q相距4个单位长度?并求出此时点P表示的数;
(3)若点P、Q以(2)中的速度同时分别从点A、B向右运动,同时点R从原点O以每秒7个单位的速度向右运动,是否存在常数m,使得2QR+3OP﹣mOR为定值,若存在请求出m值以及这个定值;若不存在,请说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,∠BAC=50°,把△ABC沿EF折叠,C对应点恰好与△ABC的外心O重合,则∠CFE的度数是( ) 
A.40°
B.45°
C.50°
D.55°
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知正方形ABCD的边长为24厘米.甲、乙两动点同时从顶点A出发,甲以2厘米/秒的速度沿正方形的边按顺时针方向移动,乙以4厘米/秒的速度沿正方形的边按逆时针方向移动,每次相遇后甲乙的速度均增加1厘米/秒且都改变原方向移动,则第四次相遇时甲与最近顶点的距离是______厘米.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知a、b分别对应数轴上A、B两点,并且满足|a﹣2|+(3a+2b)2=0,点P为数轴上一个动点,它对应的数是x
(1)填空:a= ,b= ,AB= ;
(2)若P为线段AB上一点,并且PA=3PB,求x的值;
(3)若P点从A点出发以每秒2个单位的速度运动,那么出发几秒钟后,线段PA=4PB?
![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示的图形中,所有的四边形都是正方形,所有的三角形都是直角三角形,其中最大的正方形的边长为7cm,则所有正方形的面积的和是( )cm2
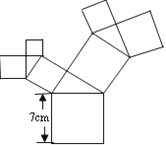
A. 28 B. 49 C. 98 D. 147
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AOB是一条直线,∠AOC=60°,OD,OE分别是∠AOC和∠BOC的平分线,则图中互补的角有( )
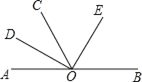
A. 5对 B. 6对 C. 7对 D. 8对
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com