
【题目】目前世界上最长的跨海大桥——杭州湾跨海大桥通车了.通车后,![]() 地到宁波港的路程比原来缩短了
地到宁波港的路程比原来缩短了![]() .已知运输车速度不变时,行驶时间将从原来的
.已知运输车速度不变时,行驶时间将从原来的![]() 缩短到
缩短到![]() .
.
(1)求![]() 地经杭州湾跨海大桥到宁波港的路程.
地经杭州湾跨海大桥到宁波港的路程.
(2)若货物运输费用包括运输成本和时间成本,某车货物从![]() 地到宁波港的运输成本是每千米
地到宁波港的运输成本是每千米![]() 元,时间成本是每时
元,时间成本是每时![]() 元,那么该车货物从
元,那么该车货物从![]() 地经杭州湾跨海大桥到宁波港的运输费用是多少元?
地经杭州湾跨海大桥到宁波港的运输费用是多少元?
(3)A地准备开辟宁波方向的外运路线,即货物从![]() 地经杭州湾跨海大桥到宁波港,再从宁波港运到
地经杭州湾跨海大桥到宁波港,再从宁波港运到![]() 地.若有一批货物(不超过
地.若有一批货物(不超过![]() 车)从
车)从![]() 地按外运路线运到
地按外运路线运到![]() 地的运费需
地的运费需![]() 元,其中从
元,其中从![]() 地经杭州湾跨海大桥到宁波港的每车运输费用与(2)中相同,从宁波港到
地经杭州湾跨海大桥到宁波港的每车运输费用与(2)中相同,从宁波港到![]() 地的海上运费对一批不超过
地的海上运费对一批不超过![]() 车的货物计费方式是:
车的货物计费方式是:![]() 车
车![]() 元,当货物每增加
元,当货物每增加![]() 车时,每车的海上运费就减少
车时,每车的海上运费就减少![]() 元,问这批货物有几车?
元,问这批货物有几车?
 优百分课时互动系列答案
优百分课时互动系列答案 开心蛙状元作业系列答案
开心蛙状元作业系列答案 课时掌控随堂练习系列答案
课时掌控随堂练习系列答案科目:初中数学 来源: 题型:
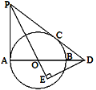
【题目】如图,AB是⊙O的直径,PA、PC与⊙O分别相切于点A,C,PC交AB的延长线于点D,DE⊥PO交PO的延长线于点E.
(1)求证:∠EPD=∠EDO;
(2)若PC=3,tan∠PDA=![]() ,求OE的长.
,求OE的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
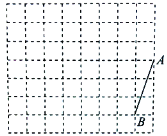
【题目】如图,方格纸中每个小正方形的边长均为1,线段AB的端点均在小正方形的顶点上.
(1)在图中画出以线段AB为一边的矩形ABCD(不是正方形),且点C和点D均在小正方形的顶点上;
(2)在图中画出以线段AB为一腰,底边长为![]() 的等腰三角形ABE,点E在小正方形的顶点,则CE= ;
的等腰三角形ABE,点E在小正方形的顶点,则CE= ;
(3)F是边AD上一动点,则CF+EF的最小值是 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】用适当的方法解下列方程.
(1)x2﹣x﹣1=0; (2)x2﹣2x=2x+1;
(3)x(x﹣2)﹣3x2=﹣1; (4)(x+3)2=(1﹣2x)2.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在矩形ABCD中,AB=4,BC=5,E是BC边上的一个动点,DF⊥AE,垂足为点F,连结CF
(1)若AE=BC
①求证:△ABE≌△DFA;②求四边形CDFE的周长;③求tan∠FCE的值;
(2)探究:当BE为何值时,△CDF是等腰三角形.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】 如图,在边长为4的正方形纸片ABCD中,从边CD上剪去一个矩形EFGH,且有EF=DH=CE=1cm,FG=2cm,动点P从点A开始沿AD边向点D以1cm/s的速度运动至点D停止.以AP为边在AP的下方做正方形AQKP,设点P运动时间为t(s),正方形AQKP和纸片重叠部分的面积为S(cm2),则S与t之间的函数关系用图象表示大致是( )
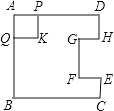
A. 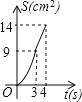 B.
B. 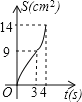
C. 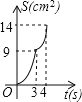 D.
D. 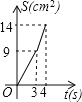
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,点A坐标为(0,3),x轴上点P(t,0),将线段AP绕点P顺时针旋转90°得到PE,过点E作直线l⊥x轴于D,过点A作AF⊥直线l于F.
(1)当点E是DF的中点时,求直线PE的函数表达式.
(2)当t=5时,求△PEF的面积.
(3)在直线l上是否存在点G,使得∠APO=∠PFD+∠PGD?若存在,试用t的代数式表示点G的坐标;若不存在,请说明理由.
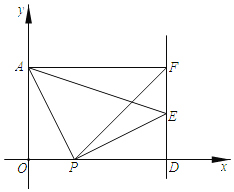
查看答案和解析>>
科目:初中数学 来源: 题型:
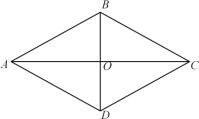
【题目】如图,在四边形ABCD中,对角线AC与BD相交于点O,AC⊥BD,AC平分∠BAD.
(1)给出下列四个条件:①AB=AD,②OB=OD,③∠ACB=∠ACD,④AD∥BC,上述四个条件中,选择一个合适的条件,使四边形ABCD是菱形,这个条件是(填写序号);
(2)根据所选择的条件,证明四边形ABCD是菱形.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com