
【题目】如图,有一个不定的正方形ABCD,它的两个相对的顶点A,C分别在边长为1的正六边形一组对边上,另外两个顶点B,D在正六边形内部(包括边界),则正方形边长a的取值范围是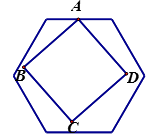
【答案】![]()
( ![]() )
)
【解析】解:因为AC为对角线,故当AC最小时,正方形边长此时最小.
①当 A、C都在对边中点时(如下图所示位置时),显然AC取得最小值,
∵正六边形的边长为1,
∴AC=![]() ,
,
∴a2+a2=AC2=![]() .
.
∴a=![]() =
=![]() .
.
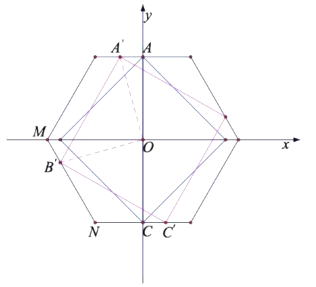
②当正方形四个顶点都在正六边形的边上时,a最大(如下图所示).
设A′(t,![]() )时,正方形边长最大.
)时,正方形边长最大.
∵OB′⊥OA′.
∴B′(-![]() , t)
, t)
设直线MN解析式为:y=kx+b,M(-1,0),N(-![]() , -
, -![]() )(如下图)
)(如下图)
∴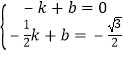 .
.
∴![]() .
.
∴直线MN的解析式为:y=![]() (x+1),
(x+1),
将B′(-![]() , t)代入得:t=
, t)代入得:t=![]() -
-![]() .
.
此时正方形边长为A′B′取最大.
∴a=![]() =3-
=3-![]() .
.
故答案为:![]() ≤a≤3-
≤a≤3-![]() .
.
分情况讨论.① 当A、C都在对边中点时,a最小.②当正方形四个顶点都在正六边形的边上时,a最大.根据题意求出正方形对角线的长度,再根据勾股定理即可求出a.从而得出a的范围.


 冲刺100分1号卷系列答案
冲刺100分1号卷系列答案科目:初中数学 来源: 题型:
【题目】已知,△ABC 是等腰直角三角形,BC=AB,A 点在 x 负半轴上,直角顶点 B 在 y 轴上,点 C 在 x 轴上方.
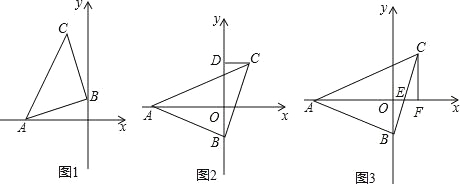
(1)如图1所示,若A的坐标是(﹣3,0),点 B的坐标是(0,1),求点 C 的坐标;
(2)如图2,过点 C 作 CD⊥y 轴于 D,请直接写出线段OA,OD,CD之间等量关系;
(3)如图3,若 x 轴恰好平分∠BAC,BC与 x 轴交于点 E,过点 C作 CF⊥x 轴于 F,问 CF 与 AE 有怎样的数量关系?并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校要从甲、乙两名同学中挑选一人参加创新能力大赛,在最近的五次选拔测试中, 他俩的成绩分别如下表,请根据表中数据解答下列问题:
第 1 次 | 第 2 次 | 第 3 次 | 第 4 次 | 第 5 次 | 平均分 | 众数 | 中位数 | 方差 | |
甲 | 60 分 | 75 分 | 100 分 | 90 分 | 75 分 | 80 分 | 75 分 | 75 分 | 190 |
乙 | 70 分 | 90 分 | 100 分 | 80 分 | 80 分 | 80 分 | 80 分 |
(1)把表格补充完整:
(2)在这五次测试中,成绩比较稳定的同学是多少;若将 80 分以上(含 80 分) 的成绩视为优秀,则甲、乙两名同学在这五次测试中的优秀率分别是多少;
(3)历届比赛表明,成绩达到80分以上(含 80分)就很可能获奖,成绩达到 90分以上(含90分)就很可能获得一等奖,那么你认为选谁参加比赛比较合适?说明你的理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
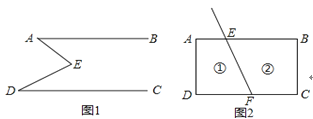
【题目】如图1,E是直线AB,CD内部一点,AB∥CD,连接EA,ED.
(1)探究猜想:①若∠A=30°,∠D=40°,则∠AED等于多少度?
②若∠A=20°,∠D=60°,则∠AED等于多少度?
③猜想图1中∠AED,∠EAB,∠EDC的关系并证明你的结论.
(2)拓展应用:如图2,线段FE与长方形ABCD的边AB交于点E,与边CD 交于点F.图2中①②分别是被线段FE隔开的2个区域(不含边界),P是位于以上两个区域内的一点,猜想∠PEB,∠PFC,∠EPF的关系(不要求说明理由).
查看答案和解析>>
科目:初中数学 来源: 题型:
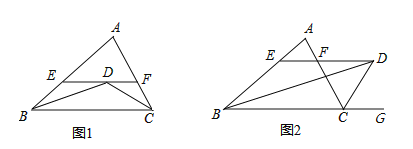
【题目】(1)如图1所示,在△ABC中,EF∥BC,点D在EF上,BD、CD分别平分∠ABC、∠ACB,若已知BE=3,CF=5,求EF的长度;
(2)如图2所示,BD平分∠ABC、CD平分∠ACG,DE∥BC交AB于点E,交AC于点F,线段EF与BE、CF有什么数量关系?并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小军同学在学校组织的社会调查活动中负责了解他所居住的小区450户居民的生活用水情况,他从中随机调查了50户居民的月均用水量(单位:t),并绘制了样本的频数分布表和频数分布直方图(如图).
(1)请根据题中已有的信息补全频数分布表和频数分布直方图;
月均用水量/t | 频数 | 百分比 |
2≤x<3 | 2 | 4% |
3≤x<4 | 12 | 24% |
4≤x<5 | ||
5≤x<6 | 10 | 20% |
6≤x<7 | 12% | |
7≤x<8 | 3 | 6% |
8≤x<9 | 2 | 4% |

(2)如果家庭月均用水量“大于或等于4 t且小于7 t”为中等用水量家庭,请你通过样本估计总体中的中等用水量家庭大约有多少户.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图, ![]() 是
是 ![]() 的中线,
的中线, ![]() 是线段
是线段 ![]() 上一点(不与点
上一点(不与点 ![]() 重合).
重合). ![]() 交
交 ![]() 于点
于点 ![]() ,
, ![]() ,连结
,连结 ![]() .
.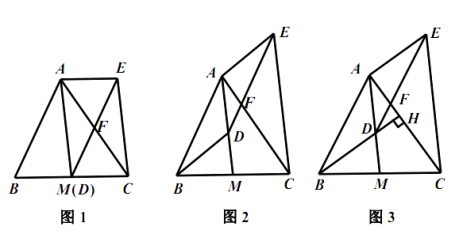
(1)如图1,当点 ![]() 与
与 ![]() 重合时,求证:四边形
重合时,求证:四边形 ![]() 是平行四边形;
是平行四边形;
(2)如图2,当点 ![]() 不与
不与 ![]() 重合时,(1)中的结论还成立吗?请说明理由.
重合时,(1)中的结论还成立吗?请说明理由.
(3)如图3,延长 ![]() 交
交 ![]() 于点
于点 ![]() ,若
,若 ![]() ,且
,且 ![]() .当
.当 ![]() ,
, ![]() 时,求
时,求 ![]() 的长.
的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在直角坐标系中,过原点O及点A(8,0),C(0,6)作矩形OABC,连结OB,D为OB的中点。点E是线段AB上的动点,连结DE,作DF⊥DE,交OA于点F,连结EF。已知点E从A点出发,以每秒1个单位长度的速度在线段AB上移动,设移动时间为t秒。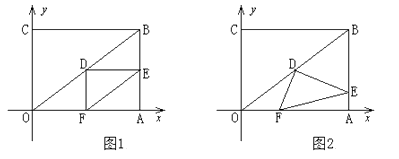
(1)如图1,当t=3时,求DF的长;
(2)如图2,当点E在线段AB上移动的过程中,∠DEF的大小是否发生变化?如果变化,请说明理由;如果不变,请求出tan∠DEF的值;
(3)连结AD,当AD将△DEF分成的两部分面积之比为1:2时,求相应t的值。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在一个不透明袋子中有1个红球、1 个绿球和n个白球,这些球除颜色外都相同.
(1)从袋中随机摸出1个球,记录下颜色后放回袋子中并搅匀,不断重复该试验.发现摸到白球的频率稳定在0.75,则n的值为;
(2)当n=2时,把袋中的球搅匀后任意摸出2个球,求摸出的2个球颜色不同的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com