
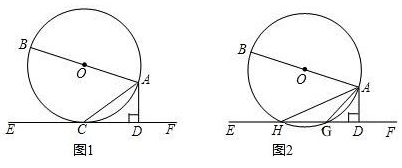
·ÖĪö £Ø1£©Į¬½ÓOC£®Ö»ŅŖÖ¤Ć÷”ĻACD+”ĻOAC=90”ć£¬”ĻCAD+”ĻACD=90”ć¼“æɽā¾öĪŹĢā£®
£Ø2£©ČēĶ¼2ÖŠ£¬Į¬½ÓBH£®Ź×ĻČÖ¤Ć÷”ĻAGD=”ĻB£¬ÓÉ”ĻB+”ĻBAH=90”ć£¬”ĻGAD+”ĻAGD=90”ć£¬¼“æÉÖ¤Ć÷£®
£Ø3£©ŌŚRt”÷ABHÖŠ£¬Ź×ĻČĒó³öAH”¢BH£¬ÓÉHAĘ½·Ö”ĻBAG£¬ĶĘ³ö$\widehat{BH}$=$\widehat{GH}$£¬ĶĘ³öBH=HG=2£¬ÓÉ”÷ABH”×”÷AGD£¬
ĶĘ³ö$\frac{AD}{DG}$=$\frac{AH}{BH}$=$\frac{4}{2}$=2£¬ĶĘ³öAD=2DG£¬ÉčDG=x£¬ŌņAD=2x£¬ŌŚRt”÷AHDÖŠ£¬øł¾ŻAH2=AD2+DH2£¬æɵĆ42=£Ø2x£©2+£Ø2+x£©2£¬½ā·½³Ģ¼“æÉ£®
½ā“š £Ø1£©Ö¤Ć÷£ŗČēĶ¼1ÖŠ£¬Į¬½ÓOC£®
”ßEFŹĒ”ŃOµÄĒŠĻߣ¬
”ąOC”ĶEF£¬
”ą”ĻOCA+”ĻACD=90”ć£¬
”ßOC=OA£¬
”ą”ĻOCA=”ĻOAC£¬
”ą”ĻACD+”ĻOAC=90”ć£¬
”ßAD”ĶCD£¬
”ą”ĻADC=90”ć£¬
”ą”ĻCAD+”ĻACD=90”ć£¬
”ą”ĻBAC=CAD£®
£Ø2£©Ö¤Ć÷£ŗČēĶ¼2ÖŠ£¬Į¬½ÓBH£®
”ß”ĻB+”ĻAGH=180”ć£¬”ĻAGH+”ĻAGD=180”ć£¬
”ą”ĻAGD=”ĻB£¬
”ßABŹĒÖ±¾¶£¬
”ą”ĻAHB=90”ć£¬
”ą”ĻB+”ĻBAH=90”ć£¬
”ß”ĻGAD+”ĻAGD=90”ć£¬
”ą”ĻBAH=”ĻGAD£®
£Ø3£©½ā£ŗŌŚĶ¼2ÖŠ£¬ŌŚRt”÷ABHÖŠ£¬AB=2$\sqrt{5}$£¬cos”ĻBAH=$\frac{2\sqrt{5}}{5}$£¬
AH=AB•cosBAH=2$\sqrt{5}$•$\frac{2\sqrt{5}}{5}$=4£¬BH=$\sqrt{A{B}^{2}-A{H}^{2}}$=2£¬
”ßHAĘ½·Ö”ĻBAG£¬
”ą$\widehat{BH}$=$\widehat{GH}$£¬
”ąBH=HG=2£¬
”ß”ĻBHA=”ĻGAD£¬”ĻAHB=”ĻADG=90”ć£¬
”ą”÷ABH”×”÷AGD£¬
”ą$\frac{AD}{DG}$=$\frac{AH}{BH}$=$\frac{4}{2}$=2£¬
”ąAD=2DG£¬ÉčDG=x£¬ŌņAD=2x£¬
ŌŚRt”÷AHDÖŠ£¬
”ßAH2=AD2+DH2£¬
”ą42=£Ø2x£©2+£Ø2+x£©2£¬
½āµĆx=$\frac{6}{5}$»ņ2£ØÉįĘś£©£¬
”ąDG=$\frac{6}{5}$£®
µćĘĄ ±¾Ģāæ¼²éŌ²×ŪŗĻĢā”¢ĒŠĻߵĊŌÖŹ”¢ĻąĖĘČż½ĒŠĪµÄÅŠ¶ØŗĶŠŌÖŹ”¢¹“¹É¶ØĄķ”¢Čń½ĒČż½ĒŗÆŹżµČÖŖŹ¶£¬½āĢāµÄ¹Ų¼üŹĒѧ»įĢķ¼Ó³£ÓĆøØÖśĻߣ¬Ń§»į¹¹½Ø·½³Ģ½ā¾öĪŹĢā£¬ŹōÓŚÖŠæ¼Ń¹ÖįĢā£®



| Äź¼¶ | øßÖŠæĪ³Ģ | Äź¼¶ | ³õÖŠæĪ³Ģ |
| øßŅ» | øßŅ»Ćā·ŃæĪ³ĢĶĘ¼ö£” | ³õŅ» | ³õŅ»Ćā·ŃæĪ³ĢĶĘ¼ö£” |
| ø߶ž | ø߶žĆā·ŃæĪ³ĢĶĘ¼ö£” | ³õ¶ž | ³õ¶žĆā·ŃæĪ³ĢĶĘ¼ö£” |
| øßČż | øßČżĆā·ŃæĪ³ĢĶĘ¼ö£” | ³õČż | ³õČżĆā·ŃæĪ³ĢĶĘ¼ö£” |
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗĢīæÕĢā
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ½ā“šĢā
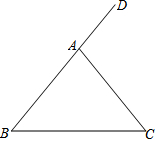 ČēĶ¼£¬ŌŚ”÷ABCÖŠ£¬AB=AC£¬”ĻDACŹĒ”÷ABCµÄŅ»øöĶā½Ē£®
ČēĶ¼£¬ŌŚ”÷ABCÖŠ£¬AB=AC£¬”ĻDACŹĒ”÷ABCµÄŅ»øöĶā½Ē£®²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ½ā“šĢā
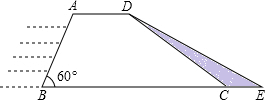 Ė®Ąū²æĆžö¶Ø¶ŌijĖ®æā“ó°Ó½ųŠŠ¼Ó¹Ģ£¬“ó°ÓµÄŗį½ŲĆęŹĒĢŻŠĪABCD£®ČēĶ¼ĖłŹ¾£¬ŅŃÖŖÓĖ®ĘĀĆęABµÄ³¤ĪŖ4Ć×£¬”ĻB=60”ć£¬±³Ė®ĘĀĆęCDµÄ³¤ĪŖ4$\sqrt{3}$Ć×£¬¼Ó¹Ģŗó“ó°ÓµÄŗį½ŲĆ껿ĪŖĢŻŠĪABED£¬CEµÄ³¤ĪŖ2Ć×£®
Ė®Ąū²æĆžö¶Ø¶ŌijĖ®æā“ó°Ó½ųŠŠ¼Ó¹Ģ£¬“ó°ÓµÄŗį½ŲĆęŹĒĢŻŠĪABCD£®ČēĶ¼ĖłŹ¾£¬ŅŃÖŖÓĖ®ĘĀĆęABµÄ³¤ĪŖ4Ć×£¬”ĻB=60”ć£¬±³Ė®ĘĀĆęCDµÄ³¤ĪŖ4$\sqrt{3}$Ć×£¬¼Ó¹Ģŗó“ó°ÓµÄŗį½ŲĆ껿ĪŖĢŻŠĪABED£¬CEµÄ³¤ĪŖ2Ć×£®²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗĢīæÕĢā
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ½ā“šĢā
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ½ā“šĢā

²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗĢīæÕĢā
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ½ā“šĢā

²éæ““š°øŗĶ½āĪö>>
°Ł¶ČÖĀŠÅ - Į·Ļ°²įĮŠ±ķ - ŹŌĢāĮŠ±ķ
ŗž±±Ź”»„ĮŖĶųĪ„·ØŗĶ²»Į¼ŠÅĻ¢¾Ł±ØĘ½ĢØ | ĶųÉĻÓŠŗ¦ŠÅĻ¢¾Ł±Ø×ØĒų | µēŠÅÕ©Ę¾Ł±Ø×ØĒų | É꥜Ź·ŠéĪŽÖ÷ŅåÓŠŗ¦ŠÅĻ¢¾Ł±Ø×ØĒų | ÉęĘóĒÖČؾŁ±Ø×ØĒų
Ī„·ØŗĶ²»Į¼ŠÅĻ¢¾Ł±Øµē»°£ŗ027-86699610 ¾Ł±ØÓŹĻä£ŗ58377363@163.com