
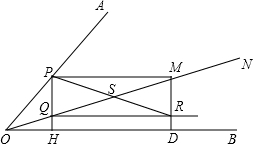
 如图,ON为∠AOB中的一条射线,点P在边OA上,PH⊥OB于H,交ON于点Q,PM∥OB交ON于点M,MD⊥OB于点D,QR∥OB交MD于点R,连接PR交QM于点S.
如图,ON为∠AOB中的一条射线,点P在边OA上,PH⊥OB于H,交ON于点Q,PM∥OB交ON于点M,MD⊥OB于点D,QR∥OB交MD于点R,连接PR交QM于点S. PR,试探究∠AOB与∠BON的数量关系,并说明理由.
PR,试探究∠AOB与∠BON的数量关系,并说明理由. PR,
PR, PR,
PR, PR,然后求出OP=PS,根据等边对等角的性质可得∠POS=∠PSO,再根据两直线平行,同位角相等可得∠SQR=∠BON,根据三角形的一个外角等于与它不相邻的两个内角的和求出∠PSO=2∠SQR,然后整理即可得解.
PR,然后求出OP=PS,根据等边对等角的性质可得∠POS=∠PSO,再根据两直线平行,同位角相等可得∠SQR=∠BON,根据三角形的一个外角等于与它不相邻的两个内角的和求出∠PSO=2∠SQR,然后整理即可得解.

科目:初中数学 来源: 题型:
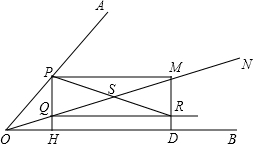 如图,ON为∠AOB中的一条射线,点P在边OA上,PH⊥OB于H,交ON于点Q,PM∥OB交ON于点M,MD⊥OB于点D,QR∥OB交MD于点R,连接PR交QM于点S.
如图,ON为∠AOB中的一条射线,点P在边OA上,PH⊥OB于H,交ON于点Q,PM∥OB交ON于点M,MD⊥OB于点D,QR∥OB交MD于点R,连接PR交QM于点S.| 1 | 2 |
查看答案和解析>>
科目:初中数学 来源: 题型:
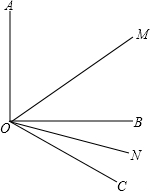 (1)如图,已知∠AOB=90°,∠BOC=30°,OM平分∠AOC,ON平分∠BOC,求∠MON的度数.
(1)如图,已知∠AOB=90°,∠BOC=30°,OM平分∠AOC,ON平分∠BOC,求∠MON的度数.查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题
| 1 |
| 2 |
查看答案和解析>>
科目:初中数学 来源:月考题 题型:单选题

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com