
 如图,△ABC中,∠C=90°,∠1=∠2,BC=6cm,DC=2$\sqrt{3}$cm,求AB、AC的长.
如图,△ABC中,∠C=90°,∠1=∠2,BC=6cm,DC=2$\sqrt{3}$cm,求AB、AC的长. 分析 根据勾股定理,可得BD的长,根据直角三角形的性质,可得∠2的度数,再根据角平分线的性质,可得∠ABC的度数,根据直角三角形的性质,可得∠A的度数,AB的长,再根据勾股定理,可得AC的长.
解答 解:在Rt△BCD中,由勾股定理,得
BD=$\sqrt{C{B}^{2}+C{D}^{2}}$=$\sqrt{{6}^{2}+(2\sqrt{3})^{2}}$=4$\sqrt{3}$.
由BD=2CD,∠C=90°,得
∠2=30°.
由∠1=∠2,得∠ABC=60°.
由直角三角形两锐角互余,得
∠A=30°.
由30°的角所对的直角边是斜边的一半,得
AB=2BC=12,
在Rt△ABC中,由勾股定理,得
AC=$\sqrt{A{B}^{2}-B{C}^{2}}$=$\sqrt{1{2}^{2}-{6}^{2}}$=6$\sqrt{3}$.
点评 本题考查了勾股定理,利用了直角三角形的性质:30°的角所对的直角边是斜边的一半,又利用了勾股定理:两直角边的平方和等于斜边的平方.


 活力试卷系列答案
活力试卷系列答案 课课优能力培优100分系列答案
课课优能力培优100分系列答案科目:初中数学 来源: 题型:填空题
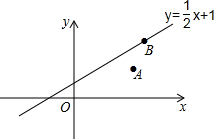 如图,B(6,4)在函数y=$\frac{1}{2}$x+1的图象上,A(5,2),点C在x轴上,点D在函数y=$\frac{1}{2}$x+1上,以A、B、C、D四个点为顶点构成平行四边形,写出所有满足条件的D点的坐标(2,2)或 D(-6,-2)、D(10,6).
如图,B(6,4)在函数y=$\frac{1}{2}$x+1的图象上,A(5,2),点C在x轴上,点D在函数y=$\frac{1}{2}$x+1上,以A、B、C、D四个点为顶点构成平行四边形,写出所有满足条件的D点的坐标(2,2)或 D(-6,-2)、D(10,6).查看答案和解析>>
科目:初中数学 来源: 题型:选择题

| A. | $\frac{{n}^{2}}{2}$ | B. | $\frac{n(n+1)}{2}$ | C. | $\frac{n(n-1)}{2}$ | D. | $\frac{(n+1)(n+2)}{2}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 45° | B. | 75° | C. | 45°或15°或75° | D. | 60° |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 某市为了改善市区交通状况,计划在康富路的北端修建通往资江北岸的新大桥,如图,新大桥的两端位于A、B两点,小张为了测量A、B之间的河宽,在垂直于新大桥AB的直线型道路l上测得如下数据:∠BDA=76.1°,∠BCA=68.2°,CD=82米.
某市为了改善市区交通状况,计划在康富路的北端修建通往资江北岸的新大桥,如图,新大桥的两端位于A、B两点,小张为了测量A、B之间的河宽,在垂直于新大桥AB的直线型道路l上测得如下数据:∠BDA=76.1°,∠BCA=68.2°,CD=82米.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com