
【题目】如图,在平面直角坐标系中,直线l的函数表达式为![]() ,点
,点![]() 的坐标为
的坐标为![]() ,以
,以![]() 为圆心,
为圆心,![]() 为半径画圆,交直线l于点
为半径画圆,交直线l于点![]() ,交x轴正半轴于点
,交x轴正半轴于点![]() ,以
,以![]() 为圆心,
为圆心,![]() 为半径画圆,交直线l于点
为半径画圆,交直线l于点![]() ,交x轴正半轴于点
,交x轴正半轴于点![]() ,以
,以![]() 为圆心,
为圆心,![]() 为半径画圆,交直线l于点
为半径画圆,交直线l于点![]() ,交x轴正半轴于点
,交x轴正半轴于点![]() ;
;![]() 按此做法进行下去,其中
按此做法进行下去,其中![]() 的长为______.
的长为______.

【答案】22015π
【解析】
连接P1O1,P2O2,P3O3,易求得PnOn垂直于x轴,可得![]() 为
为![]() 圆的周长,再找出圆半径的规律即可解题.
圆的周长,再找出圆半径的规律即可解题.
连接P1O1,P2O2,P3O3…
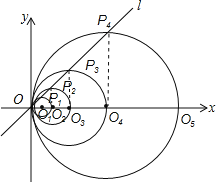
∵P1是⊙O2上的点,
∴P1O1=OO1,
∵直线l解析式为y=x,
∴∠P1OO1=45°,
∴△P1OO1为等腰直角三角形,即P1O1⊥x轴,
同理,PnOn垂直于x轴,
∴![]() 为
为![]() 圆的周长,
圆的周长,
∵以O1为圆心,O1O为半径画圆,交x轴正半轴于点O2,以O2为圆心,O2O为半径画圆,交x轴正半轴于点O3,以此类推,
∴OOn=2n-1,
∴![]() =
=![]() 2πOOn=
2πOOn=![]() π2n-1=2n-2π,
π2n-1=2n-2π,
当n=2017时,![]() =22015π.
=22015π.
故答案为 22015π.


 寒假大串联黄山书社系列答案
寒假大串联黄山书社系列答案 寒假创新型自主学习第三学期寒假衔接系列答案
寒假创新型自主学习第三学期寒假衔接系列答案科目:初中数学 来源: 题型:
【题目】已知:如图,∠1=∠2,则不一定能使△ABD≌△ACD的条件是 ( )

A. AB=AC B. BD=CD C. ∠B=∠C D. ∠BDA=∠CDA
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AB=AC,E在线段AC上,D在AB的延长线,连DE交BC于F,过点E作EG⊥BC于G.
(1)若∠A=50°,∠D=30°,求∠GEF的度数;
(2)若BD=CE,求证:FG=BF+CG.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,∠AOB=30°,M、N分别是边OA、OB上的定点,P、Q分别是边OB、OA上的动点,记∠AMP=∠1,∠ONQ=∠2,当MP+PQ+QN最小时,则关于∠1、∠2的数量关系正确的是( )

A.∠1+∠2=90°B.2∠2-∠1=30°
C.2∠1+∠2=180°D.∠1-∠2=90°
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,![]() 的顶点A(0,3),B(b,0),C(c,0)在x轴上,若
的顶点A(0,3),B(b,0),C(c,0)在x轴上,若![]() 。
。
(1)请判断![]() 的形状并予以证明;
的形状并予以证明;
(2)如图,过AB上一点D作射线交y轴负半轴与点E,连CD交y轴与F点。若BD=FD,求![]() 度数。
度数。
(3)在(2)的条件下,![]() ,H是AB延长线上一动点,作
,H是AB延长线上一动点,作![]() ,HG交射线DE于点G点,则
,HG交射线DE于点G点,则![]() 的值是否变化?若变化,请说明理由;若不变,请求出该值。
的值是否变化?若变化,请说明理由;若不变,请求出该值。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为积极响应南充市创建“全国卫生城市”的号召,某校1 500名学生参加了卫生知识竞赛,成绩记为A、B、C、D四等。从中随机抽取了部分学生成绩进行统计,绘制成如下两幅不完整的统计图表,根据图表信息,以下说法不正确的是( )
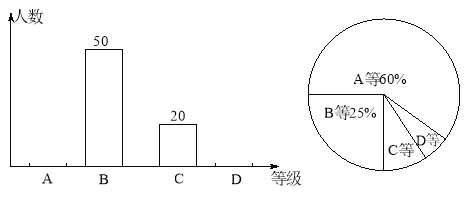
A.样本容量是200
B.D等所在扇形的圆心角为15°
C.样本中C等所占百分比是10%
D.估计全校学生成绩为A等大约有900人
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商场新进一批A、B两种型号的节能防近视台灯,每台进价分别为200元、170元,近两周的销售情况如下:
销售时段 | 销售数量 | 销售收入 | |
A种型号 | B种型号 | ||
第一周 | 3台 | 5台 | 1800元 |
第二周 | 4台 | 10台 | 3100元 |
![]() 进价、售价均保持不变,利润
进价、售价均保持不变,利润![]() 销售收入
销售收入![]() 进货成本
进货成本![]()
![]() 求A、B两种型号的台灯的销售单价;
求A、B两种型号的台灯的销售单价;
![]() 若该商场准备用不多于5400元的金额再购进这两种型号的台灯共30台,求A种型号的台灯最多能购进多少台?
若该商场准备用不多于5400元的金额再购进这两种型号的台灯共30台,求A种型号的台灯最多能购进多少台?
![]() 在
在![]() 的条件下,能否求出该商场销售完这30台台灯所获得的最大利润
的条件下,能否求出该商场销售完这30台台灯所获得的最大利润![]() 若能,求出最大利润;若不能,请说明理由.
若能,求出最大利润;若不能,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知关于x的一元二次方程mx2-2x+1=0.
(1)若方程有两个实数根,求m的取值范围;
(2)若方程的两个实数根为x1,x2,且x1x2-x1-x2=![]() ,求m的值.
,求m的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线y=ax2+bx-3a经过A(-1,0),C(0,-3)两点,与x轴交于另一点B.
(1)求此抛物线的表达式;
(2)已知点D(m,-m-1)在第四象限的抛物线上,求点D关于直线BC对称的点D′的坐标;
(3)在(2)的条件下,连接BD.问在x轴上是否存在点P,使∠PCB=∠CBD?若存在,请求出P点的坐标;若不存在,请说明理由.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com