
【题目】已知关于x的一元二次方程x2+3x+1﹣m=0有两个不相等的实数根.
(1)求m的取值范围;
(2)若m为负整数,求此时方程的根.
【答案】(1)m>﹣![]() .(2)x1=﹣1和x2=﹣2.
.(2)x1=﹣1和x2=﹣2.
【解析】试题分析:(1)由方程有两个不等实数根可得b2﹣4ac>0,代入数据即可得出关于m的一元一次不等式,解不等式即可得出结论;
(2)根据m为负整数以及(1)的结论可得出m的值,将其代入原方程,利用分解因式法解方程即可得出结论.
试题解析:(1)∵关于x的一元二次方程x2+3x+1﹣m=0有两个不相等的实数根,
∴△=b2﹣4ac=32﹣4(1﹣m)>0,
即5+4m>0,解得:m>﹣![]() .
.
∴m的取值范围为m>﹣![]() .
.
(2)∵m为负整数,且m>﹣![]() ,∴m=﹣1.
,∴m=﹣1.
将m=﹣1代入原方程得:x2+3x+2=(x+10)(x+2)=0,
解得:x1=﹣1,x2=﹣2.
故当m=﹣1时,此方程的根为x1=﹣1和x2=﹣2.


科目:初中数学 来源: 题型:
【题目】如图,池塘边有一块长为20米,宽为10米的长方形土地,现在将其余三面留出宽都是x米的小路,中间余下的长方形部分做菜地,用代数式表示: 
(1)菜地的长a=米,菜地的宽b=米;菜地的面积S=平方米;
(2)x=1时,求菜地的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】计算题计算:
(1)(﹣ ![]() ﹣
﹣ ![]() +
+ ![]() ﹣
﹣ ![]() +
+ ![]() )×(﹣60)
)×(﹣60)
(2)﹣23﹣(1﹣0.5)× ![]() ×[2﹣(﹣3)2]
×[2﹣(﹣3)2]
(3)(4x2y﹣3xy2)﹣(1+4x2y﹣3xy2)
(4)5(a2b﹣2ab2+c)﹣4(2c+3a2b﹣ab2)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在一次800米的长跑比赛中,甲、乙两人所跑的路程s(米)与各自所用时间t(秒)之间的函数图象分别为线段OA和折线OBCD,则下列说法正确的是( )
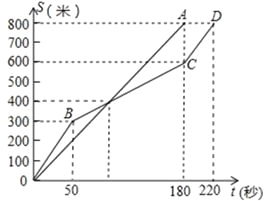
A. 甲的速度随时间的增加而增大
B. 乙的平均速度比甲的平均速度大
C. 在起跑后第180秒时,两人相遇
D. 在起跑后第50秒时,乙在甲的前面
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com