
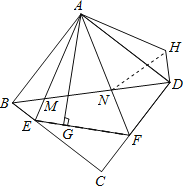
【题目】如图,△AEF中,∠EAF=45°,AG⊥EF于点G,现将△AEG沿AE折叠得到△AEB,将△AFG沿AF折叠得到△AFD,延长BE和DF相交于点C.
(1)求证:四边形ABCD是正方形;
(2)连接BD分别交AE、AF于点M、N,将△ABM绕点A逆时针旋转,使AB与AD重合,得到△ADH,试判断线段MN、ND、DH之间的数量关系,并说明理由.
(3)若EG=4,GF=6,BM=3![]() ,求AG、MN的长.
,求AG、MN的长.

【答案】(1)证明见解析;(2)MN2=ND2+DH2,理由见解析;(3)![]()
【解析】
(1)由图形翻折变换的性质可知∠ABE=∠AGE=∠BAD=∠ADC=90°,AB=AD即可得出结论;
(2)连接NH,由△ABM≌△ADH,得AM=AH,BM=DH,∠ADH=∠ABD=45°,故∠NDH=90°,再证△AMN≌△AHN,得MN=NH,由勾股定理即可得出结论;
(3)设AG=x,则EC=x-4,CF=x-6,在Rt△ECF中,利用勾股定理即可得出AG的值,同理可得出BD的长,设NH=y,在Rt△NHD,利用勾股定理即可得出MN的值.
(1)证明:∵△AEB由△AED翻折而成,
∴∠ABE=∠AGE=90°,∠BAE=∠EAG,AB=AG,
∵△AFD由△AFG翻折而成,
∴∠ADF=∠AGF=90°,∠DAF=∠FAG,AD=AG,
∵∠EAG+∠FAG=∠EAF=45°,
∴∠ABE=∠AGE=∠BAD=∠ADC=90°,
∴四边形ABCD是矩形,
∵AB=AD,
∴四边形ABCD是正方形;
(2)MN2=ND2+DH2,
理由:连接NH,
∵△ADH由△ABM旋转而成,
∴△ABM≌△ADH,
∴AM=AH,BM=DH,
∵由(1)∠BAD=90°,AB=AD,
∴∠ADH=∠ABD=45°,
∴∠NDH=90°,
∵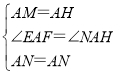 ,
,
∴△AMN≌△AHN,
∴MN=NH,
∴MN2=ND2+DH2;
(3)设AG=BC=x,则EC=x-4,CF=x-6,
在Rt△ECF中,
∵CE2+CF2=EF2,即(x-4)2+(x-6)2=100,x1=12,x2=-2(舍去)
∴AG=12,
∵AG=AB=AD=12,∠BAD=90°,
∴BD=![]() =
=![]() ,
,
∵BM=3![]() ,
,
∴MD=BD-BM=12![]() -3
-3![]() =9
=9![]() ,
,
设NH=y,
在Rt△NHD中,
∵NH2=ND2+DH2,即y2=(9![]() -y)2+(3
-y)2+(3![]() )2,解得y=5
)2,解得y=5![]() ,即MN=5
,即MN=5![]() .
.


科目:初中数学 来源: 题型:
【题目】如图,DB∥AC,且DB=![]() AC,E是AC的中点.
AC,E是AC的中点.

(1)求证:四边形BDEC是平行四边形;
(2)连接AD、BE,△ABC添加一个条件: ,使四边形DBEA是矩形(不需说明理由).
查看答案和解析>>
科目:初中数学 来源: 题型:
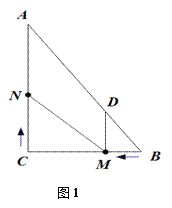
【题目】如图1,在Rt△ABC中,∠C=90,BC=6,AC=8.动点M从点B开始沿边BC向点C以每秒1个单位长度的速度运动,动点N从点C开始沿边CA向点A以每秒2个单位长度的速度运动,点M、N同时出发,且当其中一点到达端点时,另一点也随之停止运动.过点M作MD∥AC,交AB于点D,连接MN.设运动时间为t秒(t≥0).
(1)当t为何值时,四边形ADMN为平行四边形?
(2)是否存在t的值,使四边形ADMN为菱形?若存在,求出t的值;若不存在,说明理由.并探究只改变点N的速度(匀速运动),使四边形ADMN在某一时刻为菱形,求点N的速度;
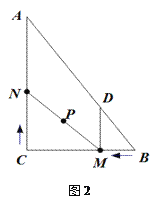
(3)如图2,在整个运动过程中,求出线段MN中点P所经过的路径长.
查看答案和解析>>
科目:初中数学 来源: 题型:
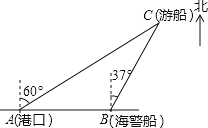
【题目】 一艘观光游船从港口A以北偏东60°的方向出港观光,航行80海里至C处时发生了侧翻沉船事故,立即发出了求救信号,一艘在港口正东方向的海警船接到求救信号,测得事故船在它的北偏东37°方向,马上以40海里每小时的速度前往救援,求海警船到大事故船C处所需的大约时间.(温馨提示:sin53°≈0.8,cos53°≈0.6)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC中,∠A=90°,AB=AC,BC=20,DE是△ABC的中位线,点M是边BC上一点,BM=3,点N是线段MC上的一个动点,连接DN,ME,DN与ME相交于点O.若△OMN是直角三角形,则DO的长是______.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】西安市2016年中考,综合素质测试满分为100分.某校为了调查学生对于综合素质的掌握程度,在九年级学生中随机抽取了部分学生进行模拟测试,并将测试成绩绘制成下面两幅统计图.
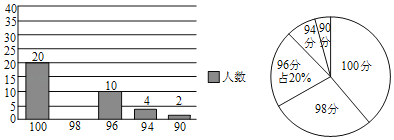
试根据统计图中提供的数据,回答下面问题:
(1)计算样本中,成绩为98分的学生有 ,并补全条形统计图.
(2)样本中,测试成绩的中位数是 分,众数是 分.
(3)若该校九年级共有2000名学生,根据此次模拟成绩估计该校九年级中考综合素质测试将有多少名学生可以获得满分.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,∠C=90°,∠B=30°,以A为圆心,任意长为半径画弧分别交AB、AC于点M和N,再分别以M、N为圆心,大于![]() MN的长为半径画弧,两弧交于点P,连接AP并延长交BC于点D,则下列说法中正确的个数是( )
MN的长为半径画弧,两弧交于点P,连接AP并延长交BC于点D,则下列说法中正确的个数是( )
①AD是∠BAC的平分线;②∠ADC=60°;③点D在AB的垂直平分线上.
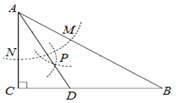
A. 3 B. 2 C. 1 D. 0
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知![]() 是
是![]() 的直径,
的直径,![]() 是
是![]() 的弦,
的弦,![]() 平分
平分![]() 交
交![]() 于点
于点![]() ,连接
,连接![]() 、
、![]() ,过点
,过点![]() 作
作![]() ,交
,交![]() 的延长线于点
的延长线于点![]() .
.
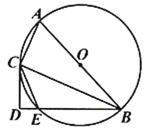
(1)![]() ________
________![]() (填“>”,“<”或“=”);
(填“>”,“<”或“=”);
(2)求证:![]() 是
是![]() 的切线;
的切线;
(3)若![]() 的直径为10,sin∠BAC=
的直径为10,sin∠BAC=![]() ,求
,求![]() 的长.
的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为落实“绿水青山就是金山银山”的发展理念,某市政部门招标一工程队负责在山脚下修建一座水库的土方施工任务.该工程队有![]() 两种型号的挖掘机,已知3台
两种型号的挖掘机,已知3台![]() 型和5台
型和5台![]() 型挖掘机同时施工一小时挖土165立方米;4台
型挖掘机同时施工一小时挖土165立方米;4台![]() 型和7台
型和7台![]() 型挖掘机同时施工一小时挖土225立方米.每台
型挖掘机同时施工一小时挖土225立方米.每台![]() 型挖掘机一小时的施工费用为300元,每台
型挖掘机一小时的施工费用为300元,每台![]() 型挖掘机一小时的施工费用为180元.
型挖掘机一小时的施工费用为180元.
(1)分别求每台![]() 型,
型, ![]() 型挖掘机一小时挖土多少立方米?
型挖掘机一小时挖土多少立方米?
(2)若不同数量的![]() 型和
型和![]() 型挖掘机共12台同时施工4小时,至少完成1080立方米的挖土量,且总费用不超过12960元.问施工时有哪几种调配方案,并指出哪种调配方案的施工费用最低,最低费用是多少元?
型挖掘机共12台同时施工4小时,至少完成1080立方米的挖土量,且总费用不超过12960元.问施工时有哪几种调配方案,并指出哪种调配方案的施工费用最低,最低费用是多少元?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com