
【题目】如图,AB是⊙O的直径,弦CD⊥AB于H,过CD延长线上一点E作⊙O的切线交AB的延长线于F.切点为G,连接AG交CD于K. 
(1)求证:KE=GE;
(2)若KG2=KDGE,试判断AC与EF的位置关系,并说明理由;
(3)在(2)的条件下,若sinE= ![]() ,AK=2
,AK=2 ![]() ,求FG的长.
,求FG的长.
【答案】
(1)解:如答图1,连接OG.
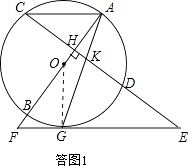
∵EG为切线,∴∠KGE+∠OGA=90°,
∵CD⊥AB,∴∠AKH+∠OAG=90°,
又OA=OG,∴∠OGA=∠OAG,
∴∠KGE=∠AKH=∠GKE,
∴KE=GE
(2)解:AC∥EF,理由为:
连接GD,如答图2所示.
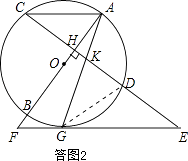
∵KG2=KDGE,即 ![]() =
= ![]() ,
,
∴ ![]() =
= ![]() ,又∠KGE=∠GKE,
,又∠KGE=∠GKE,
∴△GKD∽△EGK,
∴∠E=∠AGD,又∠C=∠AGD,
∴∠E=∠C,
∴AC∥EF
(3)解:连接OG,OC,如答图3所示.
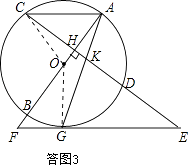
sinE=sin∠ACH= ![]() ,设AH=3t,则AC=5t,CH=4t,
,设AH=3t,则AC=5t,CH=4t,
∵KE=GE,AC∥EF,∴CK=AC=5t,∴HK=CK﹣CH=t.
在Rt△AHK中,根据勾股定理得AH2+HK2=AK2,
即(3t)2+t2=(2 ![]() )2,解得t=
)2,解得t= ![]() ,
,
设⊙O半径为r,在Rt△OCH中,OC=r,OH=r﹣3t,CH=4t,
由勾股定理得:OH2+CH2=OC2,
即(r﹣3t)2+(4t)2=r2,解得r= ![]() t=
t= ![]() .
.
∵EF为切线,∴△OGF为直角三角形,
在Rt△OGF中,OG=r= ![]() ,tan∠OFG=tan∠CAH=
,tan∠OFG=tan∠CAH= ![]() =
= ![]() ,
,
∴FG= ![]() =
= ![]() =
= ![]()
【解析】(1)如答图1,连接OG.根据切线性质及CD⊥AB,可以推出连接∠KGE=∠AKH=∠GKE,根据等角对等边得到KE=GE;(2)AC与EF平行,理由为:如答图2所示,连接GD,由∠KGE=∠GKE,及KG2=KDGE,利用两边对应成比例且夹角相等的两三角形相似可得出△GKD与△EKG相似,又利用同弧所对的圆周角相等得到∠C=∠AGD,可推知∠E=∠C,从而得到AC∥EF;(3)如答图3所示,连接OG,OC.首先求出圆的半径,根据勾股定理与垂径定理可以求解;然后在Rt△OGF中,解直角三角形即可求得FG的长度.


 愉快的寒假南京出版社系列答案
愉快的寒假南京出版社系列答案科目:初中数学 来源: 题型:
【题目】如图,原有一大长方形,被分割成3个正方形和2个长方形后仍是中心对称图形.若原来该大长方形的周长是120,则分割后不用测量就能知道周长的图形标号为( )

A. ①② B. ②③ C. ①③ D. ①②③
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在![]() 中,
中, ![]() ,将
,将![]() 绕点A顺时针旋转到
绕点A顺时针旋转到![]() 的位置,点E在斜边AB上,连结BD,过点D作
的位置,点E在斜边AB上,连结BD,过点D作![]() 于点F.
于点F.
(1)如图1,若点F与点A重合.①求证: ![]() ;②若
;②若![]() ,求出
,求出![]() ;
;
(2)若![]() ,如图2,当点F在线段CA的延长线上时,判断线段AF与线段AB的数量关系.并说明理由.
,如图2,当点F在线段CA的延长线上时,判断线段AF与线段AB的数量关系.并说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】吸烟有害健康,为配合“戒烟”运动,某校组织同学们在社区开展了“你支持哪种戒烟方式”的随机问卷调查,并将调查结果绘制成两幅不完整的统计图:据统计图解答下列问题: 
(1)同学们一共调查了多少人?
(2)将条形统计图补充完整.
(3)若该社区有1万人,请你估计大约有多少人支持“警示戒烟”这种方式?
(4)为了让更多的市民增强“戒烟”意识,同学们在社区做了两期“警示戒烟”的宣传.若每期宣传后,市民支持“警示戒烟”的平均增长率为20%,则两期宣传后支持“警示戒烟”的市民约有多少人?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AD是△ABC的高,AE是△ABC的角平分线,AF是△ABC的中线,图中相等的角有________________________________,相等的线段有__________.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,∠BAC与∠CBE的平分线相交于点P,BE=BC,PB与CE交于点H,PG∥AD交BC于F,交AB于G,下列结论:① GA=GP;② S△PAC∶S△PAB=AC∶AB;③ BP垂直平分CE;④ FP=FC,其中正确的判断有( )
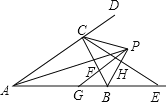
A. 只有①② B. 只有③④ C. 只有①③④ D. ①②③④
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了解某品牌电风扇销售量的情况,对某商场5月份该品牌甲、乙、丙三种型号的电风扇销售量进行统计,绘制如下两个统计图(均不完整).请你结合图中的信息,解答下列问题:
(1)该商场5月份售出这种品牌的电风扇共多少台?
(2)若该商场计划订购这三种型号的电风扇共2000台,根据5月份销售量的情况,求该商场应订购丙种型号电风扇多少台比较合理?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】二次函数y=ax2+bx+c(a≠0)的图象如图所示,下列结论:①2a+b=0;②a+c>b;③抛物线y=ax2+bx+c与x轴的另一个交点为(3,0);④abc>0.其中正确的结论是(填写序号) 
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com