
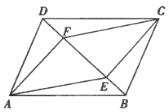
【题目】如图,在平行四边形![]() 中,
中,![]() ,
,![]() 是对角线
是对角线![]() 上不同的两点,连接
上不同的两点,连接![]() ,
,![]() ,
,![]() ,
,![]() .下列条件中,不能得出四边形
.下列条件中,不能得出四边形![]() 一定是平行四边形的为( )
一定是平行四边形的为( )
A. ![]() B.
B. ![]()
C. ![]() D.
D. ![]()
【答案】B
【解析】
连接AC与BD相交于O,然后利用平行四边形的性质和三角形全等的性质进行判别即可
如图,连接AC与BD相交于O,在平行四边形ABCD中,OA=OC,OB=OD

要使四边形AECF为平行四边形,只需证明得到OE=OF即可
A、若BE=DF,则OB-BE=OD-DF,即OE=OF,故选项不符合题意
B、若AE=CF,则无法判断OE=OF,故选项符合题意
C、AF∥CE能利用角角边证明△AOF和△COE全等,从而得到OE=OF,放选项不符合题意
D、∠BAE=∠DCF能够利用角角边证明△ABE和△CDF全等,从而得到DF=BE,然后根据A选项可得OE=OF,故选项不符合
题意
故答案为:B.


科目:初中数学 来源: 题型:
【题目】“十一”黄金周期间,淮安动物园在7天假期中每天接待的人数变化如下表(正数表示比前一天多的人数,负数表示比前一天少的人数),把9月30日的游客人数记为a万人.
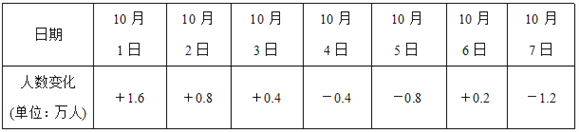
(1)请用含a的代数式表示10月2日的游客人数;
(2)请判断七天内游客人数最多的是哪天,有多少人?
(3)若9月30日的游客人数为2万人,门票每人10元,问黄金周期间淮安动物园门票收入是多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校八年级数学小组在课外活动中,研究了同一坐标系中两个反比例函数![]() 与
与![]() (
(![]() )在第一象限图像的性质,经历了如下探究过程:
)在第一象限图像的性质,经历了如下探究过程:
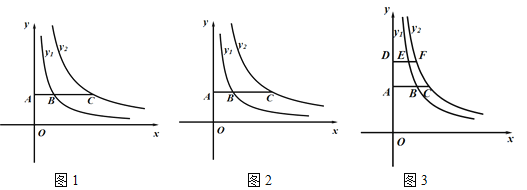
操作猜想:(1)如图1,当![]() ,
,![]() 时,在y轴的正半轴上取一点A作x轴的平行线交
时,在y轴的正半轴上取一点A作x轴的平行线交![]() 于点B,交
于点B,交![]() 于点C.当OA=1时,
于点C.当OA=1时,![]() = ;当OA=3时,
= ;当OA=3时,![]() = ;当OA=a时,猜想
= ;当OA=a时,猜想![]() = .
= .
数学思考:(2)在y轴的正半轴上任意取点A作x轴的平行线,交![]() 于点B、交
于点B、交![]() 于点C,请用含
于点C,请用含![]() 、
、![]() 的式子表示
的式子表示![]() 的值,并利用图2加以证明.
的值,并利用图2加以证明.
推广应用:(3)如图3,若![]() ,
,![]() ,在y轴的正半轴上分别取点A、D(OD>OA)作x轴的平行线,交
,在y轴的正半轴上分别取点A、D(OD>OA)作x轴的平行线,交![]() 于点B、E,交
于点B、E,交![]() 于点C、F,是否存在四边形ADFB是正方形?如果存在,求OA的长和点B的坐标;如果不存在,请说明理由.
于点C、F,是否存在四边形ADFB是正方形?如果存在,求OA的长和点B的坐标;如果不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】仔细阅读下面例题,解答问题:
例题:已知二次三项式x2-4x+m有一个因式是(x+3),求另一个因式以及m的值.
解:设另一个因式为(x+n),得x2-4x+m=(x+3)(x+n),则x2-4x+m=x2+(n+3)x+3n.
∴![]() ,
,
解得:![]() .
.
∴另一个因式为(x-7),m的值为-21.
问题:仿照以上方法解答下面问题:
(1)已知二次三项式2x2+3x-k有一个因式是(2x-5),求另一个因式以及k的值
(2)已知二次三项式6x2+4ax+2有一个因式是(2x+a),a是正整数,求另一个因式以及a的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某运输公司承担了某标段的土方运输任务,公司已派出大小两种型号的渣土运输车运输土方,已知2辆大型渣土运输车与3辆小型渣土运输车每次共35吨,3辆大型渣土运输车和2辆小型渣土运输车每次共运40吨.
(1)一辆大型渣土运输车和一辆小型渣土运输车每次各运土方多少吨?
(2)该运输公司决定派出大小两种型号的渣土运输车共20辆参与运输土方,若每次运输土方总量不小于150吨,问该运输公司最多派出几辆小型渣土运输车?
查看答案和解析>>
科目:初中数学 来源: 题型:
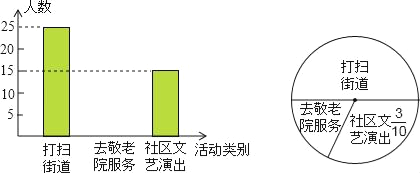
【题目】某中学组织全体学生参加“献爱心”公益活动,为了了解九年级学生参加活动情况,从九年级学生着中随机抽取部分学生进行调查,统计了该天他们打扫街道,去敬老院服务和到社区文艺演出的人数,并绘制了如下不完整的条形统计图和扇形统计图,其中到社区文艺演出的人数占所调查的九年级学生人数的![]() ,请根据两幅统计图中的信息,回答下列问题:
,请根据两幅统计图中的信息,回答下列问题:
(1)本次调查共抽取了多少名九年级学生?
(2)补全条形统计图.
(3)若该中学九年级共有1500名学生,请你估计该中学九年级去敬老院的学生有多少名?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】完成下面推理过程:
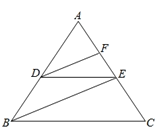
如图,已知:DE∥BC,DF、BE分别平分∠ADE、∠ABC.
求证:∠FDE=∠DEB
证明:∵DE∥BC(已知)
∴∠ADE=∠ ① ( ② )
∵DF、BE分别平分∠ADE、∠ABC,(已知)
∴∠ADF=![]() ∠ ③ ( ④ )
∠ ③ ( ④ )
∠ABE=![]() ∠ ⑥ ( ⑤ )
∠ ⑥ ( ⑤ )
∴∠ADF=∠ABE(等量代换)
∴DF∥ ( ⑦ )
∴∠FDE=∠DEB( ⑧ )
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC中,∠ABC=90°,AB=6,AC=10,∠BAC和∠ACB的平分线相交于点E,过点E作EF∥BC交AC于点F,那么EF的长为( )
[Failed to download image : http://qbm-images.oss-cn-hangzhou.aliyuncs.com/QBM/2018/4/13/1923086297137152/1923946164379648/STEM/8dc0999226e6439d82d3fa2c2424ef2e.png]
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com