
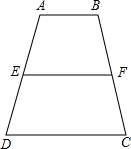
 在梯形ABCD中,AB=a,CD=b,a<b,EF为一线段,若S四边形ABFE=S四边形CDEF,且∠BFE=∠D,求EF的长(用a,b表示)
在梯形ABCD中,AB=a,CD=b,a<b,EF为一线段,若S四边形ABFE=S四边形CDEF,且∠BFE=∠D,求EF的长(用a,b表示) 分析 延长DA,CB交于点M,设△MAB=S,由AB∥CD,得到∠MAB=∠ADC,推出△MAB∽△MDC,根据相似三角形的性质得到$\frac{{S}_{△MAB}}{{S}_{△MDC}}$=$\frac{A{B}^{2}}{C{D}^{2}}$,求出S△MDC=$\frac{s{b}^{2}}{{a}^{2}}$,于是得到S梯形ABCD=S△MDC-S△MAB=$\frac{s({b}^{2}-{a}^{2})}{{a}^{2}}$,根据已知条件S四边形ABFE=S四边形CDEF,得到S四边形ABEF=$\frac{1}{2}$S梯形ABCD=$\frac{1}{2}$•$\frac{s({b}^{2}-{a}^{2})}{{a}^{2}}$,然后通过△MAB∽△MFE,求得$\frac{{S}_{△MAB}}{{S}_{△MEF}}$=$\frac{A{B}^{2}}{E{F}^{2}}$,即可得到结论.
解答  解:延长DA,CB交于点M,设△MAB=s,
解:延长DA,CB交于点M,设△MAB=s,
∵AB∥CD,
∴∠MAB=∠ADC,
∵∠M=∠M,
∴△MAB∽△MDC,
∴$\frac{{S}_{△MAB}}{{S}_{△MDC}}$=$\frac{A{B}^{2}}{C{D}^{2}}$,
即$\frac{S}{{S}_{△MDC}}$=$\frac{{a}^{2}}{{b}^{2}}$,
∴S△MDC=$\frac{s{b}^{2}}{{a}^{2}}$,
∴S梯形ABCD=S△MDC-S△MAB=$\frac{s({b}^{2}-{a}^{2})}{{a}^{2}}$,
∵S四边形ABFE=S四边形CDEF,
∴S四边形ABEF=$\frac{1}{2}$S梯形ABCD=$\frac{1}{2}$•$\frac{s({b}^{2}-{a}^{2})}{{a}^{2}}$,
∴S△MEF=S△MAB+S四边形ABEF=s+$\frac{s({b}^{2}-{a}^{2})}{2{a}^{2}}$=$\frac{s({b}^{2}+{a}^{2})}{2{a}^{2}}$,
∵∠BFE=∠ADC,
∴∠MAB=∠BFE,
∵∠M=∠M,
∴△MAB∽△MFE,
∴$\frac{{S}_{△MAB}}{{S}_{△MEF}}$=$\frac{A{B}^{2}}{E{F}^{2}}$,
即:$\frac{s}{\frac{s({b}^{2}+{a}^{2})}{2{a}^{2}}}$=$\frac{{a}^{2}}{E{F}^{2}}$,
∴EF2=$\frac{{a}^{2}+{b}^{2}}{2}$,
∴EF=$\sqrt{\frac{{a}^{2}+{b}^{2}}{2}}$.
点评 本题考查了相似三角形的判定和性质,梯形的性质,平行线的性质,正确的作出辅助线是解题的关键.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:选择题
| A. | $\overrightarrow{a}$$+\overrightarrow{b}$与$\frac{1}{2}$$\overrightarrow{a}$$+\overrightarrow{b}$$-\frac{1}{2}$$\overrightarrow{b}$ | B. | $\frac{1}{2}$($\overrightarrow{a}$$-3\overrightarrow{b}$)与$\frac{3}{2}$($\overrightarrow{a}$$-2\overrightarrow{b}$) | C. | 2$\overrightarrow{a}$$+\overrightarrow{b}$与$\overrightarrow{a}$$+\overrightarrow{b}$ | D. | 5$\overrightarrow{a}$$-3\overrightarrow{b}$与$\frac{2}{3}$$\overrightarrow{a}$$-\frac{1}{5}$$\overrightarrow{b}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | $\frac{1}{10}$(a-b) | B. | a-$\frac{1}{10}$b | C. | a+b-$\frac{1}{10}$ | D. | a-b-$\frac{1}{10}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
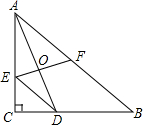 在△ABC中,∠C=90°,AC=BC,点D在BC上,DE∥AB交AC于E,点F为AB中点,连接EF.若EF⊥AD,AO=3,则OD=2.
在△ABC中,∠C=90°,AC=BC,点D在BC上,DE∥AB交AC于E,点F为AB中点,连接EF.若EF⊥AD,AO=3,则OD=2.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
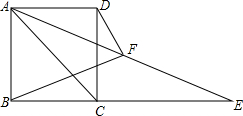 如图,矩形ABCD,过点A作∠DAC的角平分线与BC的延长线相交于点E.
如图,矩形ABCD,过点A作∠DAC的角平分线与BC的延长线相交于点E.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| x | 1.0 | 1.1 | 1.2 | 1.3 |
| x2+12x | 13 | 14.41 | 15.84 | 17.29 |
| A. | 1.0<x<1.1 | B. | 1.1<x<1.2 | C. | 1.2<x<1.3 | D. | 14.41<x<15.84 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com