
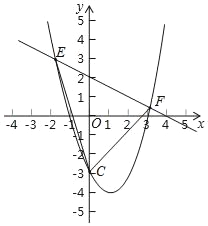
【题目】抛物线y=x2﹣2x﹣3与交y轴负半轴于C点,直线y=kx+2交抛物线于E、F两点(E点在F点左边).使△CEF被y轴分成的两部分面积差为5,则k的值为_____.
【答案】﹣4
【解析】
设直线y=kx+2交抛物线于E、F两点的横坐标分别为x1,x2,且(x1<0,x2>0),根据题意得出x1+x2=2+k,然后根据△CEF被y轴分成的两部分面积差为5,列出关于k的方程,解方程即可.
设直线y=kx+2交抛物线于E、F两点的横坐标分别为x1,x2,且(x1<0,x2>0),
由题意可知:x1,x2是方程x2-2x-3=kx+2的两个根,
整理方程为:x2-(2+k)x-5=0,
∴x1+x2=2+k,
由抛物线y=x2-2x-3可知C(0,-3),
设直线y=kx+2交y轴于B,
∴B(0,2),
∴BC=5,
∵△CEF被y轴分成的两部分面积差为5,
∴|S△BCE-S△BCF|=5,
当S△BCE-S△BCF=5时,则有![]() ×5x2-
×5x2-![]() ×5(-x1)=5,
×5(-x1)=5,
整理得:
![]() (x1+x2)=5,
(x1+x2)=5,
∴![]() (2+k)=5,解得k=0(舍去),
(2+k)=5,解得k=0(舍去),
当S△BCE-S△BCF=-5时,则有![]() ×5x2-
×5x2-![]() ×5(-x1)=-5,
×5(-x1)=-5,
整理得:![]() (x1+x2)=-5,
(x1+x2)=-5,
∴![]() (2+k)=-5,解得k=-4,
(2+k)=-5,解得k=-4,
故答案是:-4.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】一条公路旁依次有![]() 、
、![]() 、
、![]() 三个村庄,甲、乙两人骑自行车分别从
三个村庄,甲、乙两人骑自行车分别从![]() 村、
村、![]() 村同时出发前往
村同时出发前往![]() 村,甲、乙之间的距离
村,甲、乙之间的距离![]() 与骑行时间
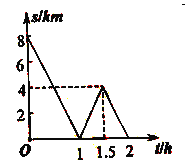
与骑行时间![]() 之间的函数关系如图所示,下列结论:
之间的函数关系如图所示,下列结论:
①![]() 、
、![]() 两村相距
两村相距![]() ;
;
②甲出发![]() 后到达
后到达![]() 村;
村;
③甲每小时比乙我骑行![]() ;
;
④相遇后,乙又骑行了![]() 或
或![]() 时两人相距
时两人相距![]() .
.
其中正确结论的个数是( )
A.1B.2C.3D.4
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知二次函数y=﹣(x﹣a)(x﹣b),其中a<b,m、n(m<n)是方程1﹣(x﹣a)(x﹣b)=0的两个根,则实数a、b、m、n的大小关系是( )
A. a<m<n<b B. m<a<b<n C. a<m<b<n D. m<a<n<b
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知某项工程由甲、乙两队合做12天可以完成,共需工程费用27720元.乙队单独完成这项工程所需时间是甲队单独完成这项工程所需时间的1.5倍,且甲队每天的工程费用比乙队多250元.
(1)求甲、乙两队单独完成这项工程各需多少天?
(2)若工程管理部门决定从这两个队中选一个队单独完成此项工程,从节约资金的角度考虑,应选择哪个工程队?请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)抛物线![]() 经过点A (4,0),点B (1,-3) ,求该抛物线的解析式;
经过点A (4,0),点B (1,-3) ,求该抛物线的解析式;
(2)如图,要修建一个圆形喷水池,在池中心竖直安装一根水管,在水管的顶端安一个喷水头,使喷出的抛物线形水柱在与池中心的水平距离为1m处达到最高,高度为3m,水柱落地处离池中心3m,水管应多长?

(3)如图,点P![]() (
(![]() >0),在
>0),在![]() 轴正半轴上,过点P作平行于
轴正半轴上,过点P作平行于![]() 轴的直线,分别交抛物线
轴的直线,分别交抛物线![]() 于点A,B,交抛物线
于点A,B,交抛物线![]() 于点C,D,求
于点C,D,求![]() 的值.
的值.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知y+2与x成正比例,且x=-2时,y=0
(1)求y与x之间的函数表达式,并画出函数的图象;
(2)利用图象直接写出:当y>0时,x的取值范围;
(3)设点P在y轴负半轴上,(2)中的图象与x轴,y轴分别交于A,B两点,且S△ABP=4,求P点的坐标
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】二次函数y=ax2+bx+c(a,b,c为常数,且a≠0)中的x与y的部分对应值如下表:

下列结论:
(1)ac<0; (2)当x>1时,y的值随x值的增大而减小.
(3)3是方程ax2+(b-1)x+c=0的一个根;(4)当-1<x<3时,ax2+(b-1)x+c>0.
其中正确的的是_________;(填序号)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知一次函数y=2x+b.
(1)它的图像与两坐标轴所围成的图形的面积等于4,求b的值;
(2)它的图像经过一次函数y=-2x+1、y=x+4图像的交点,求b的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com