
【题目】如图,某人为了测量小山顶上的塔ED的高,他在山下的点A处测得塔尖点D的仰角为45°,再沿AC方向前进60m到达山脚点B,测得塔尖点D的仰角为60°,塔底点E的仰角为30°,求塔ED的高度.(结果保留根号)

【答案】![]() .
.
【解析】
试题分析:先求出∠DBE=30°,∠BDE=30°,得出BE=DE,然后设EC=x,则BE=2x,DE=2x,DC=3x,BC=![]() x,然后根据∠DAC=45°,可得AC=CD,列出方程求出x的值,然后即可求出塔DE的高度.
x,然后根据∠DAC=45°,可得AC=CD,列出方程求出x的值,然后即可求出塔DE的高度.
试题解析:由题知,∠DBC=60°,∠EBC=30°,∴∠DBE=∠DBC﹣∠EBC=60°﹣30°=30°.
又∵∠BCD=90°,∴∠BDC=90°﹣∠DBC=90°﹣60°=30°,∴∠DBE=∠BDE,∴BE=DE.
设EC=x,则DE=BE=2EC=2x,DC=EC+DE=x+2x=3x,BC=![]() =
=![]() =
=![]() x,由题知,∠DAC=45°,∠DCA=90°,AB=20,∴△ACD为等腰直角三角形,∴AC=DC,∴
x,由题知,∠DAC=45°,∠DCA=90°,AB=20,∴△ACD为等腰直角三角形,∴AC=DC,∴![]() x+60=3x,解得:x=
x+60=3x,解得:x=![]() ,∴DE=2x=
,∴DE=2x=![]() .
.
答:塔高约为![]() m.
m.


科目:初中数学 来源: 题型:
【题目】2014年12月10日,连通杭州、南昌、长沙三座省会城市的杭长高铁开通,这给勇于创业的衢州人民的出行带来了极大的方便.杭长高铁总投资1300亿元,1300亿元用科学记数法表示为( )
A.13×1010元
B.1.3×1010元
C.0.13×1012元
D.1.3×1011元
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】“校园安全”受到全社会的广泛关注,某中学对部分学生就校园安全知识的了解程度,采用了随机抽样调查的方式,并根据收集到的信息进行统计,绘制了下面两幅尚不完整的统计图.

请你根据统计图中所提供的信息解答下列问题:
(1)接受问卷调查的学生共有 人,扇形统计图中“基本了解”部分所对应扇形的圆心角为 .
(2)请补全条形统计图.
(3)若从对校园安全知识达到“了解”程度的3个女生和2个男生中随机抽取2人参加校园安全知识竞赛,请用画树状图或列表的方法求出恰好抽到1个男生和1个女生的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
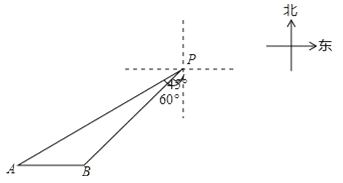
【题目】一艘轮船位于灯塔P南偏西60°方向,距离灯塔20海里的A处,它向东航行多少海里到达灯塔P南偏西45°方向上的B处(参考数据:![]() ≈1.732,结果精确到0.1)?
≈1.732,结果精确到0.1)?
查看答案和解析>>
科目:初中数学 来源: 题型:
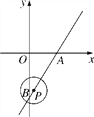
【题目】如图,在平面直角坐标系xOy中,直线y=![]() x-2
x-2![]() 与x轴、y轴分别交于A,B两点,P是直线AB上一动点,⊙P的半径为1.
与x轴、y轴分别交于A,B两点,P是直线AB上一动点,⊙P的半径为1.
(1)判断原点O与⊙P的位置关系,并说明理由;
(2)当⊙P过点B时,求⊙P被y轴所截得的劣弧的长;
(3)当⊙P与x轴相切时,求出切点的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在四边形ABCD中,AD=BC,∠B=∠D,AD不平行于BC,过点C作CE∥AD交△ABC的外接圆O于点E,连接AE.
(1)求证:四边形AECD为平行四边形;
(2)连接CO,求证:CO平分∠BCE.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com