
【题目】如图(一), ![]() 为一条拉直的细线,A、B两点在
为一条拉直的细线,A、B两点在 ![]() 上,且
上,且 ![]() :
: ![]() =1:3,
=1:3, ![]() :
: ![]() =3:5.若先固定B点,将
=3:5.若先固定B点,将 ![]() 折向
折向 ![]() ,使得
,使得 ![]() 重迭在
重迭在 ![]() 上,如图(二),再从图(二) 的A点及与A点重迭处一起剪开,使得细线分成三段,则此三段细线由小到大的长度比为何?( )
上,如图(二),再从图(二) 的A点及与A点重迭处一起剪开,使得细线分成三段,则此三段细线由小到大的长度比为何?( ) 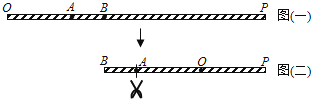
A.1:1:1
B.1:1:2
C.1:2:2
D.1:2:5
 寒假学与练系列答案
寒假学与练系列答案科目:初中数学 来源: 题型:
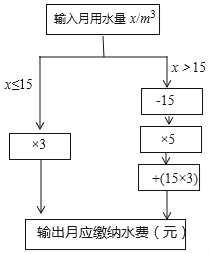
【题目】小明根据市自来水公司的居民用水收费标准,制定了水费计算数值转换机的示意图.(用水量单位:m3,水费单位:元)
(1)根据转换机程序计算下列各户月应缴纳水费
用户 | 张大爷 | 王阿姨 | 小明家 |
月用水量/m3 | 6 | 15 | 17 |
月应缴纳水费/元 |
|
|
|
(2)当x>15时,用含x的代数式表示水费 ;
(3)小丽家10月份水费是70元,小丽家10月份用水 m3.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我们学习了勾股定理后,都知道“勾三、股四、弦五”.
观察:3,4,5;5,12,13;7,24,25;9,40,41;……发现这些勾股数的勾都是奇数,且从3起就没有间断过.
(1)请你根据上述的规律写出下一组勾股数:_______________________;
(2)若第一个数用字母n(n为奇数,且n≥3)表示,则后两个数用含n的代数式表示分别为___________________。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知数轴上有A、B两个点.
(1)如图1,若AB=a,M是AB的中点,C为线段AB上的一点,且![]() ,则AC= ,CB= ,MC= (用含a的代数式表示);
,则AC= ,CB= ,MC= (用含a的代数式表示);
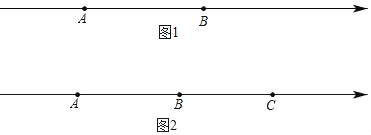
(2)如图2,若A、B、C三点对应的数分别为﹣40,﹣10,20.
①当A、C两点同时向左运动,同时B点向右运动,已知点A、B、C的速度分别为8个单位长度/秒、4个单位长度/秒、2个单位长度/秒,点M为线段AB的中点,点N为线段BC的中点,在B、C相遇前,在运动多少秒时恰好满足:MB=3BN.
②现有动点P、Q都从C点出发,点P以每秒1个单位长度的速度向终点A移动;当点P移动到B点时,点Q才从C点出发,并以每秒3个单位长度的速度向左移动,且当点P到达A点时,点Q也停止移动(若设点P的运动时间为t).当PQ两点间的距离恰为18个单位时,求满足条件的时间t值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】坐标平面上,某二次函数图形的顶点为(2,﹣1),此函数图形与x轴相交于P、Q两点,且PQ=6.若此函数图形通过(1,a)、(3,b)、(﹣1,c)、(﹣3,d)四点,则a、b、c、d之值何者为正?( )
A.a
B.b
C.c
D.d
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(10分)小慧和小聪沿图1中的景区公路游览.小慧乘坐车速为30km/h的电动汽车,早上7:00从宾馆出发,游玩后中午12:00回到宾馆.小聪骑车从飞瀑出发前往宾馆,速度为20km/h,途中遇见小慧时,小慧恰好游完一景点后乘车前往下一景点.上午10:00小聪到达宾馆.图2中的图象分别表示两人离宾馆的路程s(km)与时间t(h)的函数关系.试结合图中信息回答:

(1)小聪上午几点钟从飞瀑出发?
(2)试求线段AB、GH的交点B的坐标,并说明它的实际意义.
(3)如果小聪到达宾馆后,立即以30km/h的速度按原路返回,那么返回途中他几点钟遇见小慧?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一个小立方体的六个面分别标有字母A,B,C,D,E,F从三个不同方向看到的情形如图所示.
(1) A对面的字母是 ,B对面的字母是 ,E对面的字母是 .(请直接填写答案)

(2) 若A=2x-1,B=-3x+9.C=-7.D=1,E=4x+5,F=9,且字母A与它对面的字母表示的数互为相反数,求B,E的值
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲乙两地相距200千米,一辆客车从甲地开往乙地,一辆出租车从乙地开往甲地,两车同时出发,相向而行.已知客车的速度为60千米/小时,出租车的速度是100千米/小时.
(1)多长时间后两车相遇?
(2)若甲乙两地之间有相距50km的A、B两个加油站,当客车进入A站加油时,出租车恰好进入B站加油,求A加油站到甲地的距离.
(3)若出租车到达甲地休息10分钟后,按原速原路返回.出租车能否在到达乙地或到达乙地之前追上客车?若不能,则出租车往返的过程中,至少提速为多少才能在到达乙地或到达乙地之前追上客车?是否超速(高速限速为120千米/小时)?为什么?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,在△APE中,∠PAE=90°,PO是△APE的角平分线,以O为圆心,OA为半径作圆交AE于点G.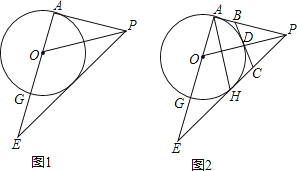
(1)求证:直线PE是⊙O的切线;
(2)在图2中,设PE与⊙O相切于点H,连结AH,点D是⊙O的劣弧 ![]() 上一点,过点D作⊙O的切线,交PA于点B,交PE于点C,已知△PBC的周长为4,tan∠EAH=
上一点,过点D作⊙O的切线,交PA于点B,交PE于点C,已知△PBC的周长为4,tan∠EAH= ![]() ,求EH的长.
,求EH的长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com