
【题目】如图(1),在![]() 中,
中,![]() ,点
,点![]() 分别是边
分别是边![]() 的中点,连接
的中点,连接![]() .
.

(1)如图①,求![]() 的值;
的值;
(2)将![]() 绕点
绕点![]() 顺时针旋转到如图(2)的位置时,
顺时针旋转到如图(2)的位置时,![]() 的大小是否发生变化,若不变化,请说明理由;若发生变化,请求出它的值;
的大小是否发生变化,若不变化,请说明理由;若发生变化,请求出它的值;
(3)将![]() 绕点
绕点![]() 顺时针旋转到直线
顺时针旋转到直线![]() 的下方,且
的下方,且![]() 在同一直线上时,如图(3),求线段
在同一直线上时,如图(3),求线段![]() 的长.
的长.
【答案】(1)![]() (2)见解析 (3)
(2)见解析 (3)![]()
【解析】
(1)利用勾股定理可求出AC的值,因此![]() ,又因为
,又因为![]() ,代入数值即可;
,代入数值即可;
(2)无变化.根据旋转的性质![]() 仍然成立,再证明△ACE∽△BCD,得出
仍然成立,再证明△ACE∽△BCD,得出![]() ,又因为
,又因为![]() ,因此,
,因此,![]() ;
;
(3)当△EDC在BC下方,且A,E,D三点共线时,△ADC为直角三角形,利用勾股定理得出![]() ,再结合已知条件即可得出AE=6,又因为
,再结合已知条件即可得出AE=6,又因为![]() ,即可得出答案.
,即可得出答案.
解:(1)在Rt△ABC中,![]() ,
,
∵AE=EC,BD=DC,∴ DE∥AB,
∴![]() ;
;
(2)无变化.
证明:在题图①中,∵DE是△ABC的中位线,
∴DE∥AB,∴![]() ,∠EDC=∠B=90°.
,∠EDC=∠B=90°.
如题图②,∵△EDC在旋转过程中形状大小不变,
∴![]() 仍然成立.
仍然成立.
又∵∠ACE=∠BCD,
∴△ACE∽△BCD,
∴![]() .
.
由(1)可知 ![]() .
.
∴![]() ,
,
∴![]() ,
,
∴![]() 的大小不变.
的大小不变.
(3)当△EDC在BC下方,且A,E,D三点共线时,△ADC为直角三角形,
如图③,由勾股定理可得![]() .
.
又DE=2,∴AE=6.
∵![]() ,∴
,∴![]() .
.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
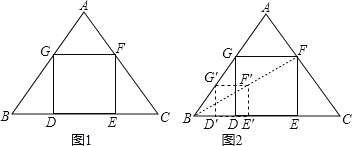
【题目】如图,△ABC是一块等边三角形的废铁片,其中AB=AC=10![]() ,BC=12
,BC=12![]() .利用其剪裁一个正方形DEFG,使正方形的一条边DE落在BC上,顶点F. G分别落在AC、AB上.
.利用其剪裁一个正方形DEFG,使正方形的一条边DE落在BC上,顶点F. G分别落在AC、AB上.
(1)小聪想:要画出正方形DEFG,只要能计算出正方形的边长就能求出BD和CE的长,从而确定D点和E点,再画正方形DEFG就容易了.请你帮小聪求出正方形的边长.
(2)小明想:不求正方形的边长也能画出正方形.具体作法是:
①在AB边上任取一点G′,如图2作正方形G′D′E′F′;
②连接BF′并延长交AC于点F;
③过点F作FE∥F′E′交BC于点E,FG∥F′G′交AB于点G,GD∥G′D′交BC于点D,则四边形DEFG即为所求的正方形.你认为小明的作法正确吗?说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
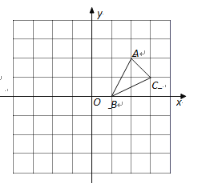
【题目】如图,△ABC的顶点的坐标分别为A(2,2),B(1,0),C(3,1)
(1)画出△ABC关于x轴对称的![]() ;
;
(2)画出△ABC绕原点O逆时针旋转90°的△A2B1C2,写出点C2的坐标;
(3)在(1)(2)的基础上,图中的![]() ,
,![]() 关于哪个点中心对称.
关于哪个点中心对称.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】文化是一个国家、一个民族的灵魂,近年来,央视推出《中国诗词大会》、《中国成语大会》、《朗读者》、《经曲咏流传》等一系列文化栏目.为了解学生对这些栏目的喜爱情况,某学校组织学生会成员随机抽取了部分学生进行调查,被调查的学生必须从《经曲咏流传》(记为A)、《中国诗词大会》(记为B)、《中国成语大会》(记为C)、《朗读者》(记为D)中选择自己最喜爱的一个栏目,也可以写出一个自己喜爱的其他文化栏目(记为E).根据调查结果绘制成如图所示的两幅不完整的统计图.
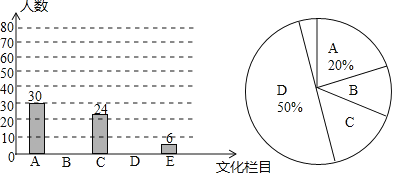
请根据图中信息解答下列问题:
(1)在这项调查中,共调查了多少名学生?
(2)将条形统计图补充完整,并求出扇形统计图中“B”所在扇形圆心角的度数;
(3)若选择“E”的学生中有2名女生,其余为男生,现从选择“E”的学生中随机选出两名学生参加座谈,请用列表法或画树状图的方法求出刚好选到同性别学生的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图是一座人行天桥的引桥部分的示意图,梯面AD、BE相互平行,且与地面成37°的夹角,DE是一段水平歇台,离地面高度3米.已知天桥高度BC为4.8米,引桥水平跨度AC为8米,求梯面AD、BE及歇台DE的长.(参考数据:![]() ,结果保留两位小数)
,结果保留两位小数)

查看答案和解析>>
科目:初中数学 来源: 题型:
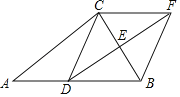
【题目】在Rt△ABC中,∠ACB=90°,点D、E分别是AB、BC的中点,过点C作CF∥AB,与DE的延长线并交于点F,连接BF.
(1)试判断四边形CDBF的形状,并说明理由;
(2)若CD=5,sin∠CAB=![]() ,过点C作CH⊥BF,垂足为H点,试求CH的长.
,过点C作CH⊥BF,垂足为H点,试求CH的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC中,∠BAC=90°,AB=3,AC=4,点D是BC的中点,将△ABD沿AD翻折得到△AED,连CE
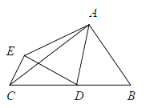
(1)求证:AD=ED
(2)连接BE,猜想△BEC的形状,并说明理由
查看答案和解析>>
科目:初中数学 来源: 题型:
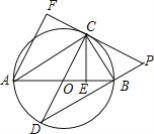
【题目】 如图,AB是⊙O的直径,点E为线段OB上一点(不与O、B重合),作EC⊥OB,交⊙O于点C,作直径CD,过点C的切线交DB的延长线于点P,作AF⊥PC于点F,连接CB.
(1)求证:AC平分∠FAB;
(2)求证:BC2=CECP;
(3)若![]() ,⊙O的面积为12π,求PF的长.
,⊙O的面积为12π,求PF的长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com