
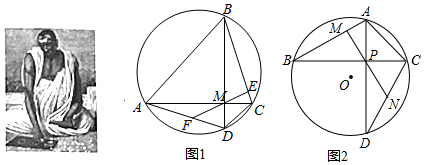
分析 (1)由于AC⊥BD,所以∠AMD=90°,∠FAM+∠FDM=90°,由于F是AD的中点,所以AF=MF=DF,从而可证明∠EMC+∠MCB=90°.
(2)由圆周角定理得出∠D=∠B=30°,由三角形内角和定理求出∠DAC=45°,得出△APC是等腰直角三角形,∴PA=PC,∠CPD=90°,由(1)的证明过程可知:PM⊥BA,再由含30°的直角三角形的性质即可求出AP=1,CD=2,最后利用直角三角形斜边上的中线等于斜边的一半即可求出PN的长度;
解答 解:(1)∵AC⊥BD,
∴∠AMD=90°,
∵F是AD的中点,
∴AF=MF=DF,
∴∠FAM=∠FMA,
∠FMD=∠FDM,
∵∠FDM=∠MCB,∠FMA=∠EMC,
∠FAM+∠FDM=90°
∴∠EMC+∠MCB=90°,
∴ME⊥BC;
(2)∵∠ACB=45°,∠BCD=60°,
∴∠ACD=45°+60°=105°,
又∵∠D=∠B=30°,
∴∠DAC=180°-∠ACD-∠D=45°,
∴∠APC=180°-45°-45°=90°,△APC是等腰直角三角形,
∴PA=PC,∠APC=90°,
∴AD⊥BC,
∵ON⊥CD,
∴由垂径定理可知:N是CD的中点,
∴由(1)的证明过程可知:PM⊥BA
∵AB=2,∠B=30°,
∴AP=1,
∴PC=1,
∵∠D=30°,
∴CD=2PC=2,
∵N是CD的中点,∠CPD=90°,
∴PN=$\frac{1}{2}$CD=1,
点评 本题考查圆的综合问题,涉及垂径定理,勾股定理,直角三角形斜边上的中线性质,含30°的直角三角形的性质等知识,综合程度较高,需要学生灵活运用知识.


 精英口算卡系列答案
精英口算卡系列答案 应用题点拨系列答案
应用题点拨系列答案 状元及第系列答案
状元及第系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
| 购票人数 | 1~50人 | 51~100人 | 100人以上 |
| 每人门票价 | 13元 | 11元 | 9元 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
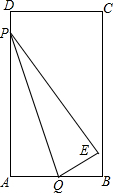 如图,矩形纸ABCD,AB=3,AD=6,动点Q从点A出发以每秒1个单位长的速度沿AB向终点B运动,运动$\frac{2}{3}$秒时,动点P从点D出发以相等的速度沿DA向终点A运动.当其中一点到达终点时,另一点也停止运动.设点P的运动时间为t(秒).将△APQ沿PQ翻折,得到△EPQ
如图,矩形纸ABCD,AB=3,AD=6,动点Q从点A出发以每秒1个单位长的速度沿AB向终点B运动,运动$\frac{2}{3}$秒时,动点P从点D出发以相等的速度沿DA向终点A运动.当其中一点到达终点时,另一点也停止运动.设点P的运动时间为t(秒).将△APQ沿PQ翻折,得到△EPQ查看答案和解析>>
科目:初中数学 来源: 题型:解答题
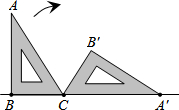 如图,一块含有30°角的直角三角板ABC,在水平桌面上绕点C按顺时针方向旋转到A′B′C的位置,若BC的长为1cm,求点A从开始到结束经过的路径长.
如图,一块含有30°角的直角三角板ABC,在水平桌面上绕点C按顺时针方向旋转到A′B′C的位置,若BC的长为1cm,求点A从开始到结束经过的路径长.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
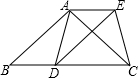 已知:如图,在△ABC中,AB=AC,D为边BC上一点,以AB,BD为邻边作平行四边形ABDE,连接AD,EC.
已知:如图,在△ABC中,AB=AC,D为边BC上一点,以AB,BD为邻边作平行四边形ABDE,连接AD,EC.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
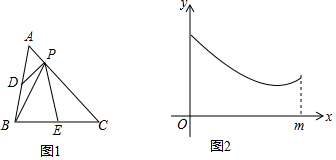
| A. | PD | B. | PB | C. | PE | D. | PC |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
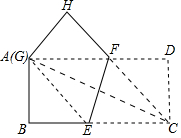 将矩形纸片ABCD(AD>AB)折叠,使点C折叠后的对应点G恰好与A点重合,且折痕分别与边BC、AD相交,设折叠后点C、D的对应点分别为点G、H,折痕分别与边BC、AD相交于点E、F.
将矩形纸片ABCD(AD>AB)折叠,使点C折叠后的对应点G恰好与A点重合,且折痕分别与边BC、AD相交,设折叠后点C、D的对应点分别为点G、H,折痕分别与边BC、AD相交于点E、F.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com