
【题目】二次函数![]() 的部分图象如图所示,图象过点
的部分图象如图所示,图象过点![]() ,对称轴为直
,对称轴为直![]() .下列结论:
.下列结论:![]() ;
;![]() ;
;![]() ;
;![]() 若点
若点![]() 点
点![]() 点
点![]() 在该函数图象上,则
在该函数图象上,则![]() ;
; ![]() 若方程
若方程![]() 的两根为
的两根为![]() 和
和![]() ,且
,且![]() ,则
,则![]() .其中正确的结论有( )
.其中正确的结论有( )

A.![]() 个B.
个B.![]() 个C.
个C.![]() 个D.
个D.![]() 个
个
【答案】B
【解析】
由题意根据对称轴公式计算得(1),利用x=-3时,y<0,即可判断(2),由图象可知抛物线经过(-1,0)和(5,0),列出方程组求出a、b即可判断(3),利用函数图象即可判断(4),利用二次函数与二次不等式关系即可判断(5).
解:(1)正确,∵![]() =2,
=2,
∴4a+b=0.故(1)正确;
(2)错误,∵x=-3时,y<0,
∴9a-3b+c<0,
∴9a+c<3b,故(2)错误;
(3)正确.由图象可知抛物线经过(-1,0)和(5,0),
∴![]() ,解得
,解得![]() ,
,
∴8a+7b+2c=8a-28a-10a=-30a,
∵a<0,
∴8a+7b+2c>0,故(3)正确;
(4)错误,∵点A(-3,y1)、点B(![]() ,y2)、点C(
,y2)、点C(![]() ,y3),
,y3),
∵![]() ,
,
∴![]() ,
,
∴点C离对称轴的距离近,
∴y3>y2,
∵a<0,-3<![]() <2,
<2,
∴y1<y2
∴y1<y2<y3,故(4)错误;
(5)正确,∵a<0,
∴(x+1)(x-5)=![]() >0,
>0,
即(x+1)(x-5)>0,
故x<-1或x>5,故(5)正确.
∴正确的有三个,
故选:B.


 课堂全解字词句段篇章系列答案
课堂全解字词句段篇章系列答案科目:初中数学 来源: 题型:
【题目】如图①,BC是⊙O的直径,点A在⊙O上,AD⊥BC垂足为D,弧AE=弧AB,BE分别交AD、AC于点F、G.
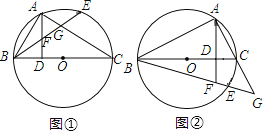
(1)判断△FAG的形状,并说明理由;
(2)如图②若点E与点A在直径BC的两侧,BE、AC的延长线交于点G,AD的延长线交BE于点F,其余条件不变(1)中的结论还成立吗?请说明理由.
(3)在(2)的条件下,若BG=26,DF=5,求⊙O的直径BC.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在正方形![]() 中,点
中,点![]() 是直线
是直线![]() 上动点,以
上动点,以![]() 为边作正方形
为边作正方形![]() ,
,![]() 所在直线与
所在直线与![]() 所在直线交于点
所在直线交于点![]() ,连接
,连接![]() .
.
(1)如图1,当点![]() 在
在![]() 边上时,延长
边上时,延长![]() 交
交![]() 于点
于点![]() ,
,![]() 与
与![]() 交于点
交于点![]() ,连接
,连接![]() .
.
①求证:![]() ;
;
②若![]() ,求
,求![]() 的值;
的值;
(2)当正方形![]() 的边长为4,
的边长为4,![]() 时,请直接写出
时,请直接写出![]() 的长.
的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】廊桥是我国古老的文化遗产.如图,是某座抛物线型的廊桥示意图,已知抛物线的函数表达式为![]() ,为保护廊桥的安全,在该抛物线上距水面
,为保护廊桥的安全,在该抛物线上距水面![]() 高为8米的点
高为8米的点![]() 、
、![]() 处要安装两盏警示灯,则这两盏灯的水平距离
处要安装两盏警示灯,则这两盏灯的水平距离![]() 是____米.
是____米.

查看答案和解析>>
科目:初中数学 来源: 题型:
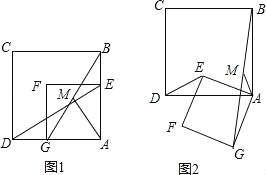
【题目】图1和图2中的正方形ABCD和四边形AEFG都是正方形.
(1)如图1,连接DE,BG,M为线段BG的中点,连接AM,探究AM与DE的数量关系和位置关系,并证明你的结论;
(2)在图1的基础上,将正方形AEFG绕点A逆时针方向旋转到图2的位置,连结DE、BG,M为线段BG的中点,连结AM,探究AM与DE的数量关系和位置关系,并证明你的结论.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图, 在等边△ABC中, D, E, F分别为边AB, BC, CA上的点, 且满足∠DEF=60°.
(1)求证:![]() ;
;
(2)若DE⊥BC且DE=EF, 求![]() 的值.
的值.
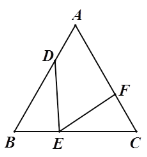
查看答案和解析>>
科目:初中数学 来源: 题型:
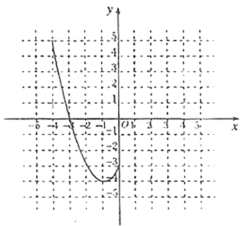
【题目】某班“数学兴趣小组”对函数![]() 的图像和性质进行了探究,探究过程如下,请补充完整.
的图像和性质进行了探究,探究过程如下,请补充完整.
(1)自变量![]() 的取值范围是全体实数,
的取值范围是全体实数,![]() 与
与![]() 的几组对应值列表如下:
的几组对应值列表如下:
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
其中,![]() ________________.
________________.
(2)根据上表数据,在如图所示的平面直角坐标系中描点,并画出了函数图像的一部分,请画出该图像的另一部分;
(3)观察函数图像,写出两条函数的性质;
(4)进一步探究函数图像发现:
①方程![]() 有______个实数根;
有______个实数根;
②函数图像与直线![]() 有_______个交点,所以对应方程
有_______个交点,所以对应方程![]() 有_____个实数根;
有_____个实数根;
③关于![]() 的方程
的方程![]() 有
有![]() 个实数根,
个实数根,![]() 的取值范围是___________.
的取值范围是___________.
查看答案和解析>>
科目:初中数学 来源: 题型:
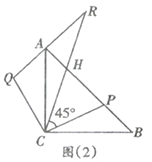
【题目】在等腰直角三角形![]() 中,
中,![]() ,
,![]() ,点
,点![]() 在斜边
在斜边![]() 上(
上(![]() ),作
),作![]() ,且
,且![]() ,连接
,连接![]() ,如图(1).
,如图(1).
(1)求证:![]() ;
;
(2)延长![]() 至点
至点![]() ,使得
,使得![]() ,
,![]() 与
与![]() 交于点
交于点![]() .如图(2).
.如图(2).
①求证:![]() ;
;
②求证:![]() .
.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com