
【题目】如图,正方形![]() 中,
中,![]() ,点
,点![]() 在边
在边![]() 上,且
上,且![]() ;将
;将![]() 沿
沿![]() 对折至
对折至![]() ,延长
,延长![]() 交边
交边![]() 于点
于点![]() ,连结
,连结![]() 、
、![]() ,下列结论中,正确的个数为( )
,下列结论中,正确的个数为( )
①![]() ;②
;②![]() ;③
;③![]() ;④
;④![]()

A.![]() 个B.
个B.![]() 个C.
个C.![]() 个D.
个D.![]() 个
个
【答案】D
【解析】
首先证明Rt△ABG≌Rt△AFG(HL),推出GB=GF,设BG=x,则GF=x,CG=BC-BG=3-x,在Rt△CGE中,GE=x+1,EC=2,CG=3-x,根据CG2+CE2=GE2,构建方程求出x即可判断①正确;
想办法证明∠AGB=∠GCF,即可判断②正确;
根据全等得出∠DAE=∠FAE,∠BAG=∠FAG.得出③正确;
只要证明![]() ,得出
,得出![]() 可得S△FCG=
可得S△FCG=![]() S△EGC,由此即可判断④正确;
S△EGC,由此即可判断④正确;
①∵四边形ABCD是正方形,
∴AB=AD=CD=3,∠B=∠D=90°,
∵CD=3,CE=2DE,
∴DE=1,
∵△ADE沿AE折叠得到△AFE,
∴DE=EF=1,AD=AF,∠D=∠AFE=∠AFG=90°,
∴AF=AB,
∵在Rt△ABG和Rt△AFG中,
AG=AG,AB=AF
∴Rt△ABG≌Rt△AFG(HL).
∴BG=FG,∠AGB=∠AGF.
设BG=x,则CG=BC-BG=3-x,GE=GF+EF=BG+DE=x+1.
在Rt△ECG中,由勾股定理得:CG2+CE2=EG2.
∵CG=3-x,CE=2,EG=x+1,
∴(3-x)2+22=(x+1)2,
解得:x=![]()
∴BG=GF=CG=![]()
即BG=CG,①正确;
②∵△ADE沿AE折叠得到△AFE,
∴△DAE≌△FAE.
∴∠DAE=∠FAE.
∵△ABG≌△AFG,
∴∠BAG=∠FAG.
∵∠BAD=90°,
∴∠EAG=∠EAF+∠GAF=![]() ×90°=45°
×90°=45°
∴②正确.
∵CG=GF,
∴∠CFG=∠FCG.
∵∠BGF=∠CFG+∠FCG,∠BGF=∠AGB+∠AGF,
∴∠CFG+∠FCG=∠AGB+∠AGF.
∵∠AGB=∠AGF,∠CFG=∠FCG,
∴∠AGB=∠FCG.
∴AG∥CF.
∴③正确;
④∵EF=DE=1,GF=![]()
∴EG=![]()
∴![]()
![]()
∴S△FGC=![]() S△EGC=
S△EGC=![]()
∴正确.
故选:D


科目:初中数学 来源: 题型:
【题目】2019年是大家公认的![]() 商用元年.移动通讯行业人员想了解
商用元年.移动通讯行业人员想了解![]() 手机的使用情况,在某高校随机对500位大学生进行了问卷调查.下列说法正确的是( )
手机的使用情况,在某高校随机对500位大学生进行了问卷调查.下列说法正确的是( )
A.该调查方式是普查
B.该调查中的个体是每一位大学生
C.该调查中的样本是被随机调查的500位大学生![]() 手机的使用情况
手机的使用情况
D.该调査中的样本容量是500位大学生
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,A,B两点在反比例函数y= ![]() 的图象上,C,D两点在反比例函数y=
的图象上,C,D两点在反比例函数y= ![]() 的图象上,AC⊥y轴于点E,BD⊥y轴于点F,AC=2,BD=1,EF=3,则k1﹣k2的值是( )
的图象上,AC⊥y轴于点E,BD⊥y轴于点F,AC=2,BD=1,EF=3,则k1﹣k2的值是( ) 
A.6
B.4
C.3
D.2
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】关于x的方程x2+(2k+1)x+k2+2=0有两个实数根x1,x2.
(1)求实数k的取值范围;
(2)若x1,x2满足|x1|+|x2|=|x1x2|-1,求k的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读下面材料:小明遇到这样一个问题;△ABC中,有两个内角相等.
①若∠A=110°,求∠B的度数;
②若∠A=40°,求∠B的度数.
小明通过探究发现,∠A的度数不同,∠B的度数的个数也可能不同,因此为同学们提供了如下解题的想法:
对于问题①,根据三角形内角和定理,∵∠A=110°>90°,∠B=∠C=35°;
对于问题②,根据三角形内角和定理,∵∠A=40°<90°,∴∠A=∠B或∠A=∠C或∠B=∠C,∴∠B的度数可求.请回答:
(1)问题②中∠B的度数为 ;
(2)参考小明解决问题的思路,解决下面问题:
△ABC中,有两个内角相等.设∠A=x°,当∠B有三个不同的度数时,求∠B的度数(用含x的代式表示)以及x的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校学生会向全校![]() 名学生发起了爱心捐款活动,为了解捐款情况,学生会随机调查了部分学生的捐款金额,并用得到的数据绘制了如下统计图1和图2,请根据相关信息,解答下列问题:
名学生发起了爱心捐款活动,为了解捐款情况,学生会随机调查了部分学生的捐款金额,并用得到的数据绘制了如下统计图1和图2,请根据相关信息,解答下列问题:
(1)本次接受随机抽样调查的学生人数为 人,图![]() 中
中![]() 的值是 .
的值是 .
(2)补全图2的统计图.
(3)求本次调查获取的样本数据的平均数、众数和中位数;
(4)根据样本数据,估计该校本次活动捐款金额为![]() 元的学生人数.
元的学生人数.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,在平面直角坐标系中,A、B,C三点的坐标分别为(0,1)、(3,3)、(4,0).
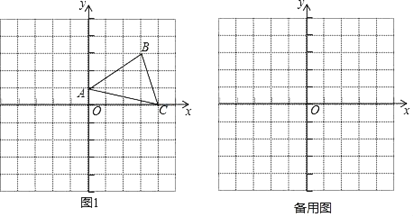
(I)S△AOC= ;
(2)若点P(m﹣1,1)是第二象限内一点,且△AOP的面积不大于△ABC的面积,求m的取值范围;
(3)若将线段AB向左平移1个单位长度,点D为x轴上一点,点E(4,n)为第一象限内一动点,连BE、CE、AC,若△ABD的面积等于由AB、BE、CE、AC四条线段围成图形的面积,则点D的坐标为 .(用含n的式子表示)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】将一个直角三角形纸板ABC放置在锐角△PMN上,使该直角三角形纸板的两条直角边AB,AC分别经过点M,N.
(发现)
(1)如图1,若点A在△PMN内,当∠P=30°时,则∠PMN+∠PNM=______°,∠AMN+∠ANM=______°,∠PMA+∠PNA=______°.
(2)如图2,若点A在△PMN内,当∠P=50°时,∠PMA+∠PNA=______°.
(探究)
(3)若点A在△PMN内,请你判断∠PMA,∠PNA和∠P之间满足怎样的数量关系,并写出理由.
(应用)
(4)如图3,点A在△PMN内,过点P作直线EF∥AB,若∠PNA=16°,则∠NPE=______.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com