【题目】某仓库甲、乙、丙三辆运货车，每辆车只负责进货或出货，每小时的运输量丙车最多，乙车最少，乙车的运输量为每小时6吨，下图是从早晨上班开始库存量y（吨）与时间x（小时）的函数图象，OA段只有甲、丙车工作，AB段只有乙、丙车工作，BC段只有甲、乙工作。
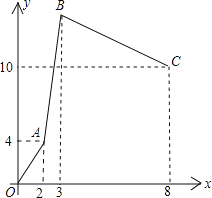
（1）甲、乙、丙三辆车中,谁是进货车?
（2）甲车和丙车每小时各运输多少吨?
（3）由于仓库接到临时通知，要求三车在8小时后同时开始工作，但丙车在运送10吨货物后出现故障而退出，问：8小时后，甲、乙两车又工作了几小时，使仓库的库存量为6吨。
【答案】(1) （1）乙、丙是进货车．(2)甲车和丙车每小时各运8吨和10吨．(3)7小时.
【解析】
试题分析：（1）根据AB段的图象以及乙车每小时运6吨，即可判断出乙、丙是进货车，则甲必是出货车．
（2）设甲、丙两车每小时运货x吨和y吨．
等量关系：①根据OA段的图象知：甲、丙两车参与运输的2小时后，仓库的库存量是4吨；
②根据A-B-C段的图象知：乙、丙两车参与运输1小时，甲、乙两车参与运输5小时后，仓库的库存量是10-4=6（吨）．
（3）设8小时后，甲、乙两车又工作了m小时，库存是6吨．根据丙车在运送10吨货物后出现故障而退出，再根据最后仓库的库存量是6吨，列方程求解．
试题解析：（1）乙、丙是进货车，甲是出货车．
（2）设甲、丙两车每小时运货x吨和y吨，
则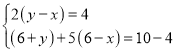
，
解得
∴甲车和丙车每小时各运8吨和10吨．
（3）设8小时后，甲、乙两车又工作了m小时，库存是6吨，则有
（8-6）m=10+10-6，
解得m=7．
答：甲、乙两车又工作了7小时，库存是6吨．
出彩同步大试卷系列答案科目：初中数学 来源： 题型：
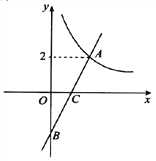
【题目】如图在平面直角坐标系xOy中，函数
（
）的图象与一次函数
的图象的交点为A（m，2）．
（1）求一次函数的解析式；
（2）观察图像直接写出使得
的
的取值范围；
（3）设一次函数y=kx-k的图象与y轴交于点B，若点P是x轴上一点，且满足△PAB的面积是4，直接写出P点的坐标.
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】下列去（添）括号做法正确的有
A. x-（y-z）=x-y-z B. -（x-y+z）=-x-y-z
C. x+2y-2z=x-2（z-y） D. –a+c+d+b=-（a+b）+（c+d）
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如果a+b<0,且ab>0,则下列结论成立的是：（ ）
A. a>0,b>0 B. a<0,b<0 C. a>0,b<0 D. a<0 ,b>0
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】已知：如图，AB∥CD，AP平分∠BAC，CP平分∠ACD，求∠APC的度数．
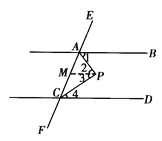
解：过P点作PM∥AB交AC于点M．
∵AB∥CD， ( )
∴∠BAC＋∠ACD＝180°． ( )
∵PM∥AB，
∴∠1＝∠_______， ( )
且PM∥_______．(平行于同一直线的两直线也互相平行)
∴∠3＝∠______． ( )
∵AP平分∠BAC，CP平分∠ACD， ( )
BAC， 
ACD．
．
∴∠APC＝∠2＋∠3＝∠1＋∠4＝90°．
总结：两直线平行时，同旁内角的角平分线______．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】在边长为1的小正方形网格中，△AOB的顶点均在格点上．
（1）B点关于y轴的对称点坐标为 ；
（2）将△AOB向左平移3个单位长度，再向上平移2个单位长度得到△A1O1B1，请画出△A1O1B1；
（3）在（2）的条件下，△AOB边AB上有一点P的坐标为（a，b），则平移后对应点P1的坐标为 ．
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com